题目内容
离心率为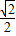 的椭圆C1的长轴两端点分别是双曲线C2:
的椭圆C1的长轴两端点分别是双曲线C2: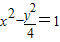 的两焦点.
的两焦点.(1)求椭圆C1的方程;
(2)直线y=x+m与椭圆C1交于A,B两点,与双曲线C2两条渐近线交于P,Q两点,且P,Q在A,B之间,使|AP|,|PQ|,|QB|成等差数列,求m的值.
【答案】分析:(1)椭圆C1的方程为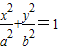 (a>b>0),根据题意列方程组,解出即可;
(a>b>0),根据题意列方程组,解出即可;
(2)由|AP|,|PQ|,|QB|成等差数列,可得|AP|+|QB|=2|PQ|,则|AB|=|AP|+|PQ|+|QB|=3|PQ|,利用弦长公式表示出|AB|,根据两点间距离公式表示出|PQ|,解此关于m方程即可.
解答:解:(1)设椭圆C1的方程为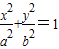 (a>b>0),
(a>b>0),
由题意知a2=1+4=5,所以a=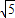 ,
,
又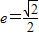 ,所以
,所以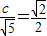 ,解得c=
,解得c=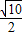 ,则b2=a2-c2=5-
,则b2=a2-c2=5- =
= .
.
故椭圆C1的方程为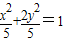 .
.
(2)由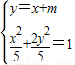 ,得3x2+4mx+2m2-5=0,
,得3x2+4mx+2m2-5=0,
设A(x1,y1),B(x2,y2),则x1+x2=-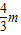 ,x1x2=
,x1x2=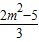 ,
,
所以|AB|=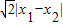 =
=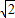 •
•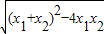 =
=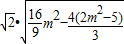 =
=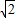 •
•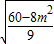 .
.
双曲线的渐近线方程为:y=2x,y=-2x,
由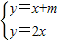 解得
解得 ,由
,由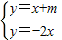 解得
解得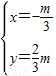 ,
,
所以两交点P,Q的坐标为(m,2m),(-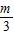 ,
,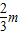 ),
),
|PQ|=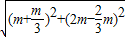 =
=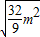 ,
,
因为|AP|,|PQ|,|QB|成等差数列,所以|AP|+|QB|=2|PQ|,所以|AB|=|AP|+|PQ|+|QB|=3|PQ|,
故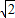 •
•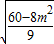 =3
=3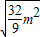 ,解得m=±
,解得m=±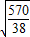 .
.
故m的值为±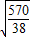 .
.
点评:本题考查椭圆的标准方程的求解及直线与圆锥曲线的位置关系问题,考查数形结合思想,考查学生分析问题解决问题的能力,直线与圆锥曲线的位置关系问题是解析几何中重要题型,弦长公式、两点间距离公式、韦达定理、判别式等解决该类问题的基础知识,须熟练掌握.
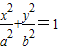 (a>b>0),根据题意列方程组,解出即可;
(a>b>0),根据题意列方程组,解出即可;(2)由|AP|,|PQ|,|QB|成等差数列,可得|AP|+|QB|=2|PQ|,则|AB|=|AP|+|PQ|+|QB|=3|PQ|,利用弦长公式表示出|AB|,根据两点间距离公式表示出|PQ|,解此关于m方程即可.
解答:解:(1)设椭圆C1的方程为
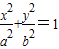 (a>b>0),
(a>b>0),由题意知a2=1+4=5,所以a=
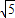 ,
,又
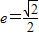 ,所以
,所以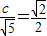 ,解得c=
,解得c=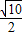 ,则b2=a2-c2=5-
,则b2=a2-c2=5- =
= .
.故椭圆C1的方程为
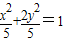 .
.(2)由
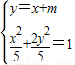 ,得3x2+4mx+2m2-5=0,
,得3x2+4mx+2m2-5=0,设A(x1,y1),B(x2,y2),则x1+x2=-
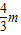 ,x1x2=
,x1x2=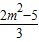 ,
,所以|AB|=
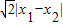 =
=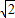 •
•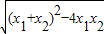 =
=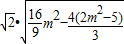 =
=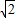 •
•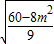 .
.双曲线的渐近线方程为:y=2x,y=-2x,
由
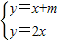 解得
解得 ,由
,由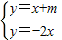 解得
解得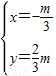 ,
,所以两交点P,Q的坐标为(m,2m),(-
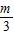 ,
,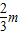 ),
),|PQ|=
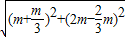 =
=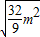 ,
,因为|AP|,|PQ|,|QB|成等差数列,所以|AP|+|QB|=2|PQ|,所以|AB|=|AP|+|PQ|+|QB|=3|PQ|,
故
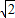 •
•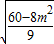 =3
=3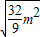 ,解得m=±
,解得m=±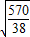 .
.故m的值为±
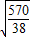 .
.点评:本题考查椭圆的标准方程的求解及直线与圆锥曲线的位置关系问题,考查数形结合思想,考查学生分析问题解决问题的能力,直线与圆锥曲线的位置关系问题是解析几何中重要题型,弦长公式、两点间距离公式、韦达定理、判别式等解决该类问题的基础知识,须熟练掌握.

练习册系列答案
相关题目
 的椭圆C1的顶点A1,A2恰好是双曲线
的椭圆C1的顶点A1,A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2. 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值.
,求实数m的值. 的椭圆C1的左、右焦点分别为F1,F2,抛物线C2:y2=4mx(m>0)的焦点为F2,设椭圆C1与抛物线C2的一个交点为P(x',y'),
的椭圆C1的左、右焦点分别为F1,F2,抛物线C2:y2=4mx(m>0)的焦点为F2,设椭圆C1与抛物线C2的一个交点为P(x',y'),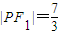 ,则椭圆C1的标准方程为 ;抛物线C2的标准方程为 .
,则椭圆C1的标准方程为 ;抛物线C2的标准方程为 . 的椭圆C1的顶点A1,A2恰好是双曲线
的椭圆C1的顶点A1,A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2. 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值.
,求实数m的值. 的椭圆C1的顶点,A1、A2恰好是双曲线
的椭圆C1的顶点,A1、A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1、A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2。
的左右焦点,点P是椭圆上不同于A1、A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2。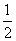 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值。
,求实数m的值。