题目内容
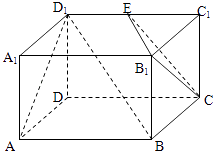
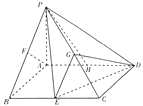
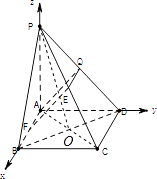
【题目】如图，在四棱锥中P﹣ABCD，底面ABCD为边长为 
的正方形，PA⊥BD． 
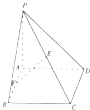
（1）求证：PB=PD；
（2）若E，F分别为PC，AB的中点，EF⊥平面PCD，求直线PB与平面PCD所成角的大小．
【答案】
（1）解：连接AC，BD交于点O，连结PO．
∵底面ABCD是正方形，
∴AC⊥BD，OB=OD．
又PA⊥BD，PA平面PAC，AC平面PAC，PA∩AC=A，
∴BD⊥平面PAC，∵PO平面PAC，
∴BD⊥PO．
又OB=OD，
∴PB=PD
（2）解：设PD的中点为Q，连接AQ，EQ，
则EQ∥CD，EQ= 
CD，又AF∥CD，AF= 
= 
，
∴EQ∥AF，EQ=AF，
∴四边形AQEF为平行四边形，∴EF∥AQ，
∵EF⊥平面PCD，∴AQ⊥平面PCD，
∴AQ⊥PD，∵Q是PD的中点，
∴AP=AD= 
．
∵AQ⊥平面PCD，∴AQ⊥CD，
又AD⊥CD，AQ∩AD=A，
∴CD⊥平面PAD，∴CD⊥PA．
又BD⊥PA，BD∩CD=D，
∴PA⊥平面ABCD．
以A为坐标原点，以AB，AD，AP为坐标轴建立如图所示的空间直角坐标系，
则B（ ，0，0），P（0，0， ），A（0，0，0），Q（0， 
， ）．
∴ 
=（0， ， ）， 
=（ ，0，﹣ ）．
∵AQ⊥平面PCD，∴ 为平面PCD的一个法向量．
∴cos＜ 
＞= 
=﹣ ．
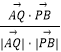设直线PB与平面PCD所成角为θ，
则sinθ=|cos＜ ＞|= ．
∴直线PB与平面PCD所成角为 
．
【解析】（1）连接AC，BD交于点O，连结PO，则AC⊥BD，结合PA⊥BD得出BD⊥平面PAC，故而BD⊥PO，又O为BD的中点，得出OP为BD的中垂线，得出结论；（2）设PD的中点为Q，连接AQ，EQ，证明四边形AQEF是平行四边形，于是AQ⊥平面PCD，通过证明CD⊥平面PAD得出CD⊥PA，结合PA⊥BD得出PA⊥平面ABCD，以A为原点建立空间直角坐标系，则直线PB与平面PCD所成角的正弦值等于|cos＜ ＞|，从而得出线面角的大小．
【考点精析】认真审题，首先需要了解空间角的异面直线所成的角(已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则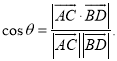
)．
