题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,且2acosA=ccosB+bcosC.
(1)求角A;
(2)若a=
,求b+c的取值范围.
(1)求角A;
(2)若a=
| 3 |
考点:正弦定理
专题:计算题,三角函数的求值,解三角形
分析:(1)运用正弦定理和两角和的正弦公式,化简三角函数式,即可得到A;
(2)由正弦定理,求出b=2sinB,c=2sinC,运用两角和的正弦公式,化简b+c,再由正弦函数的图象和性质,即可得到所求范围.
(2)由正弦定理,求出b=2sinB,c=2sinC,运用两角和的正弦公式,化简b+c,再由正弦函数的图象和性质,即可得到所求范围.
解答:
解:(1)∵2acosA=ccosB+bcosC
∴2sinAcosA=sinCcosB+sinBcosC=sin(B+C)=sinA
∴cosA=
,(0<A<π),
∴A=
;
(2)由(1)知B+C=
,0<B<
,
又∵a=
由正弦定理b=
=2sinB,c=2sinC,
∴b+c=2(sinB+sinC)=2(sinB+sin(
-B))=3sinB+
cosB
=2
sin(B+
),
∵0<B<
∴
<B+
<
,即有
<sin(B+
)≤1,
∴b+c的范围是(
,2
].
∴2sinAcosA=sinCcosB+sinBcosC=sin(B+C)=sinA
∴cosA=
| 1 |
| 2 |
∴A=
| π |
| 3 |
(2)由(1)知B+C=
| 2π |
| 3 |
| 2π |
| 3 |
又∵a=
| 3 |
由正弦定理b=
| asinB |
| sinA |
∴b+c=2(sinB+sinC)=2(sinB+sin(
| 2π |
| 3 |
| 3 |
=2
| 3 |
| π |
| 6 |
∵0<B<
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
∴b+c的范围是(
| 3 |
| 3 |
点评:本题考查正弦定理的运用,考查三角函数的恒等变换应用,考查正弦函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
若|
|=2,|
|=1,
和
夹角为60°,则|
+2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、3 | ||
D、2
|
若曲线 y=x2 上P点处的切线平行于 2x-y+1=0,则点P的坐标是( )
| A、( 1,-1) |
| B、(-1,1) |
| C、( 1,1) |
| D、(-1,-1) |
直线3x-4y-9=0与圆x2+y2=4的位置关系是( )
| A、相交且过圆心 | B、相切 |
| C、相离 | D、相交但不过圆心 |
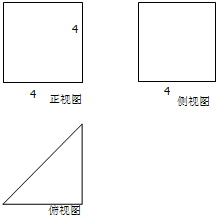 一个几何体的三视图如图所示,则这个几何体的表面积等于
一个几何体的三视图如图所示,则这个几何体的表面积等于