题目内容
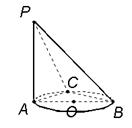
20.(本小题满分8分)如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC = 30°,PA = AB.
 (1)求证:平面PAC⊥平面PBC;
(1)求证:平面PAC⊥平面PBC;
(2)求直线PC与平面ABC所成角的正切值;
(3)求二面角A—PB—C的正弦值.
【答案】
解:(1)证明:∵AB是直径 ∴∠ACB = 90°,即BC⊥AC
∴PA⊥BC
∴BC⊥平面PAC 又BC 平面PBC
平面PBC
∴平面PBC⊥平面PAC
(2)∵PA⊥平面ABC
∴直线PC与平面ABC所成角即∠PCA
设AC = 1,∵∠ABC = 30°∴PA = AB = 2
∴tan∠PCA = = 2
(3) 在平面PAC中作AD⊥PC于D,在平面PAB中作AE⊥PB于连结DE
 ∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∴AD⊥平面PBC
∴AD⊥PB
又∵PB⊥AE ∴PB⊥面AED
∴PB⊥ED
∴∠DEA即为二面角A—PB—C的平面角
在直角三角形PAC中和直角三角形PAB中,
分别由等面积方法求得
AD = AE =
∴在直角三角形ADE中可求得:sin∠DEA =
即二面角A—PB—C的正弦值为.
【解析】略

练习册系列答案
相关题目
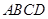 为梯形,
为梯形,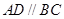 ,
,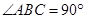 ,求图中阴影部分绕
,求图中阴影部分绕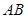 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。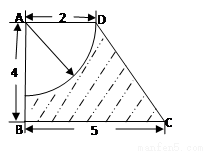
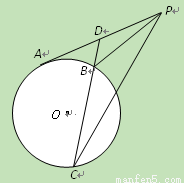
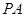 切⊙O于点
切⊙O于点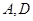 为
为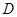 引割线交⊙O于
引割线交⊙O于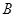 、
、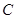 两点.求证:
两点.求证: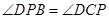 .
.
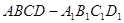 的棱长是2,
的棱长是2,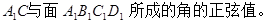

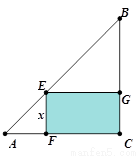
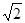 ,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
,点E是斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为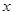 ,
,
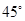 .求点A到平面PBC的距离.
.求点A到平面PBC的距离.