题目内容
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.
(1)求证:DE⊥平面BCE;
(2)求二面角A﹣EB﹣C的大小.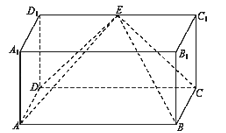
【答案】(1)证明:建立如图所示的空间直角坐标系,
则D(0,0,0),E(0,1,1),
B(1,2,3),C(0,2,0),
∴![]() =(0,1,1),
=(0,1,1),![]() =(﹣1,﹣1,1),
=(﹣1,﹣1,1),![]() =(﹣1,0,0),
=(﹣1,0,0),
∵![]()
![]()
![]() =0,
=0,![]()
![]()
![]() =0,
=0,
∴DE⊥BE,DE⊥BC,
∵BE平面BCE,BC平面BCE,BE∩BC=B,
∴DE⊥平面BCE.
(2)解:设平面AEB的法向量![]() =(x,y,z),
=(x,y,z),
则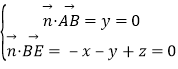 ,
,
取x=1,得![]() =(1,0,1),
=(1,0,1),
∵DE⊥平面BCE,∴![]() =(0,1,1)是平面BCE的法向量,
=(0,1,1)是平面BCE的法向量,
∵cos<![]() ,
,![]() >=
>=![]() =
=![]() ,
,
∴二面角A﹣EB﹣C的大小为120°.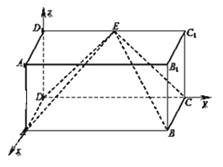
【解析】(1)建立如图所示的空间直角坐标系,利用向量法能证明DE⊥平面BCE.
(2)求出平面AEB的法向量和平面BCE的法向量,再利用向量法求出二面角A﹣EB﹣C的大小.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).

练习册系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此做了四次实验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程y= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工6个零件需要多少时间?
(注: ![]() =
= 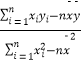 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
