题目内容
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的余弦值为
.
| ||
| 3 |
| ||
| 3 |
分析:先设出侧棱长为l,正三棱锥的底边长为a,利用异面直线所成角的概念及已知的所成角为45°建立l和a的方程,解出棱长l用a表示,再利用直线与平面所成角的概念可知SD与平面ABC所成的线面角即为∠SDO,然后在三角形SDO中求出此角的余弦值即可.
解答:解:由题意画出图形:由于三棱锥S-ABC为正三棱锥,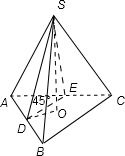
设侧棱为l,底面边长为a,因为D是AB的中点,且SD与BC成45°角,
如图取AC的中点E,因为DE∥BC,所以∠SDE=45°,
在直角三角形SDE可以得到l=
a,
在直角三角形SOD中,OD=
a,SD=
a,SO=
a,
因为SD与平面ABC所成的线面角即为∠SDO,
所以SD与底面ABC所成角的余弦值为cos∠SDO=
=
故答案为:
.

设侧棱为l,底面边长为a,因为D是AB的中点,且SD与BC成45°角,
如图取AC的中点E,因为DE∥BC,所以∠SDE=45°,
在直角三角形SDE可以得到l=
|
在直角三角形SOD中,OD=
| ||
| 6 |
|
|
因为SD与平面ABC所成的线面角即为∠SDO,
所以SD与底面ABC所成角的余弦值为cos∠SDO=
| OD |
| SD |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题重点考查了异面直线所成角的概念,考查直线与平面所成的线面角的概念及解题过程中方程的解题思想,属于中档题,解题的关键就是寻找线面所成角.

练习册系列答案
相关题目
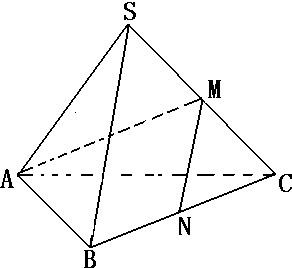 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|