题目内容
(本题9分)
已知函数f(x)=2cosx(sinx-cosx)+1。
(1)求函数f(x)的最小值以及取最小值时x的取值;
(2)求函数f(x)的单调递增区间。
已知函数f(x)=2cosx(sinx-cosx)+1。
(1)求函数f(x)的最小值以及取最小值时x的取值;
(2)求函数f(x)的单调递增区间。
解:f(x)=2cosx·sinx-2cos2x+1=sin2x-cos2x= sin(2x-
sin(2x-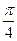 )
)
(1)f(x)min=- ,2x-
,2x-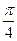 =2k
=2k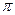 -
-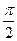 ,x=k
,x=k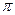 -
-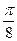 . (k
. (k Z)
Z)
(2)2k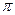 -
-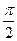 ≤2x
≤2x -
-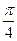 ≤2k
≤2k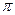 +
+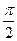 , k
, k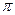 -
-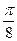 ≤x≤k
≤x≤k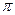 +
+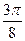 .(
.( k
k Z)
Z)
∴单调增区间为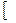 k
k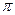 -
-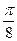 , k
, k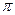 +
+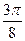
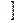 .(k
.(k Z)
Z)
 sin(2x-
sin(2x-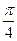 )
)(1)f(x)min=-
 ,2x-
,2x-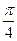 =2k
=2k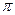 -
-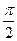 ,x=k
,x=k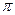 -
-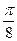 . (k
. (k Z)
Z)(2)2k
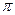 -
-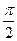 ≤2x
≤2x -
-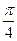 ≤2k
≤2k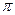 +
+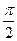 , k
, k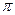 -
-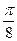 ≤x≤k
≤x≤k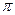 +
+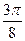 .(
.( k
k Z)
Z)∴单调增区间为
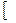 k
k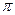 -
-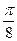 , k
, k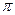 +
+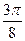
 .(k
.(k Z)
Z)略

练习册系列答案
相关题目
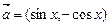 ,
,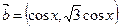 ,函数
,函数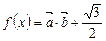
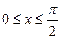 时,求函数f(x)的值域.
时,求函数f(x)的值域.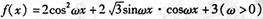 的最小正周期为
的最小正周期为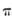
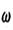 的值;
的值;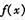 的单调区间
的单调区间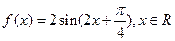
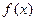 的最小正周期和单调增区间;
的最小正周期和单调增区间;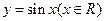 的图
的图 像经过怎样的变换得到?
像经过怎样的变换得到?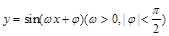 的图象的一部分
的图象的一部分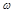 、
、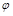 的值分别为()
的值分别为()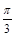
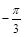
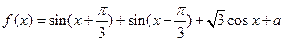 的最大值为3
的最大值为3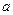 的值;
的值;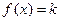 在
在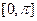 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数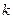 的取值范围
的取值范围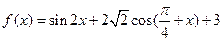 的最小值是
的最小值是 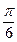 )(ω>0)的最小正周期是
)(ω>0)的最小正周期是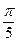 ,则ω=_________。
,则ω=_________。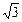 tan20°tan40°的值是 ;
tan20°tan40°的值是 ;