题目内容
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设x,y,z分别表示甲、乙、丙3个盒中的球数.
(1)求x,y,z依次成公差大于0的等差数列的概率;
(2)求至少有一个盒子没有球的概率.
解:(1)设掷出1点为事件A,掷出2点或3点事件B,掷出4点或5点或6点为事件C,
则 .
.
要使x,y,z成公差大小0的等差数列,则x=0,y=1,z=2,∴所求概率为 .(4分)
.(4分)
(2)至少有一个盒子没有球与三人盒有均有球互为对立事件
三个盒中均有球,即每人盒里有且只有一球
故所求概率为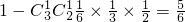 .(12分)
.(12分)
分析:(1)x,y,z依次成公差大于0的等差数列,由于前后共掷3次,则x=0,y=1,z=2,由已知中掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,分别求出甲乙丙三人盒中放球的概率,代入相互独立事件概率乘法公式,即可得到答案.
(2)先求出三人盒子中均有球,即三个盒子中各有一球的概率,然后根据对立事件概率减法公式,即可得到答案.
点评:本题考查的知识点是概率的应用,相互独立事件概率乘法公式,及对立事件概率减法公式,其中分析出满足条件的事件性质的情况,并分析出是分类还是分步,并选择恰当的概率公式,是解答此类问题的关键.
则
 .
.要使x,y,z成公差大小0的等差数列,则x=0,y=1,z=2,∴所求概率为
 .(4分)
.(4分)(2)至少有一个盒子没有球与三人盒有均有球互为对立事件
三个盒中均有球,即每人盒里有且只有一球
故所求概率为
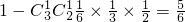 .(12分)
.(12分)分析:(1)x,y,z依次成公差大于0的等差数列,由于前后共掷3次,则x=0,y=1,z=2,由已知中掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,分别求出甲乙丙三人盒中放球的概率,代入相互独立事件概率乘法公式,即可得到答案.
(2)先求出三人盒子中均有球,即三个盒子中各有一球的概率,然后根据对立事件概率减法公式,即可得到答案.
点评:本题考查的知识点是概率的应用,相互独立事件概率乘法公式,及对立事件概率减法公式,其中分析出满足条件的事件性质的情况,并分析出是分类还是分步,并选择恰当的概率公式,是解答此类问题的关键.

练习册系列答案
相关题目
 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。 的概率;
的概率; 求随机变量
求随机变量 的分布列和数学期望。
的分布列和数学期望。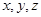 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.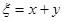 ,求随机变量
,求随机变量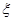 的概率分布列和数学期望.
的概率分布列和数学期望.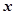 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。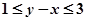 的概率;
的概率;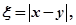 求随机变量
求随机变量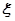 的分布列和数学期望。
的分布列和数学期望。