题目内容
在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球,若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设x,y z 分别表示甲,乙,丙3个盒中的球数.
(1)求x,y,z依次成公差大于0的等差数列的概率;
(2)记ξ=x+y,求随机变量ξ的概率分布列和数学期望.
(1)求x,y,z依次成公差大于0的等差数列的概率;
(2)记ξ=x+y,求随机变量ξ的概率分布列和数学期望.
分析:(1)x,y,z依次成公差大于0的等差数列的概率,即甲,乙,丙3个盒中的球数.分别为0,1,2,由此能求出其概率.
(2)把两盒的球合并成一盒.则每次掷骰子后球放入该盒中的概率p=
+
=
,且ξ~B(3,
),由此能求出随机变量ξ的概率分布列数学期望.
(2)把两盒的球合并成一盒.则每次掷骰子后球放入该盒中的概率p=
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)x,y,z依次成公差大于0的等差数列的概率,
即甲,乙,丙3个盒中的球数.
分别为0,1,2,
此时的概率p=
×
×(
)2=
.(6分)
(2)解:把两盒的球合并成一盒.
则每次掷骰子后球放入该盒中的概率p=
+
=
,
且ξ~B(3,
),
随机变量ξ的概率分布列
Eξ=3×
=
.(13分)
即甲,乙,丙3个盒中的球数.
分别为0,1,2,
此时的概率p=
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)解:把两盒的球合并成一盒.
则每次掷骰子后球放入该盒中的概率p=
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
且ξ~B(3,
| 1 |
| 2 |
随机变量ξ的概率分布列
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意二项分布的性质和应用.

练习册系列答案
相关题目
 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。 的概率;
的概率; 求随机变量
求随机变量 的分布列和数学期望。
的分布列和数学期望。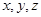 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.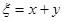 ,求随机变量
,求随机变量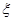 的概率分布列和数学期望.
的概率分布列和数学期望.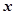 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。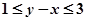 的概率;
的概率;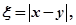 求随机变量
求随机变量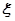 的分布列和数学期望。
的分布列和数学期望。