题目内容
（本小题满分12分）已知函数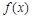
的定义域为R，对任意的实数
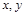都有
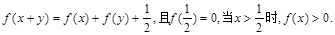
（1）求f(1)；
（2）判断函数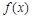的增减性并证明；
【答案】
（1）f(1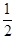)=f(
)+f()+=.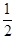
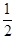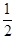（2）f(x)在R上是增函数。
【解析】（1）令x=y=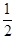，得f(1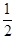)=f()+f(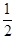)+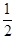=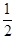.……………………………………5分
（2）任取x1，x2∈R，且x2＞x1,Δx=x2-x1＞0，则
Δy=f(x2)-f(x1)=f(x1+Δx)-f(x1)=f(Δx)+f(x1)+ 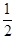-f(x1)=f(Δx)+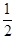
= f (Δx)+ 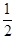+f(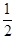)=f(Δx+)
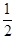又Δx＞0，∴Δx+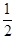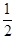＞，由题知f(Δx+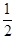)＞0，即f(x2)＞f(x1)，
所以f(x)在R上是增函数………………………………………………………………12分
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
