题目内容
已知函数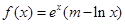 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数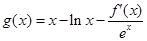 的最小值为1,其中
的最小值为1,其中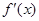 是函数f(x)的导数.
是函数f(x)的导数.
(1)求m的值.
(2)判断直线y=e是否为曲线f(x)的切线,若是,试求出切点坐标和函数f(x)的单调区间;若不是,请说明理由.
(1) 1 ;(2)是,(1,e);单调减区间(0,+∞).
解析试题分析:(1)求导数,转化为分式不等式,最后根据不等式的基本性质求解即可.(2)利用导数的几何意义,求过(1,e)的切线即可验证.
试题解析:由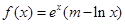 ,得
,得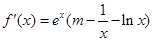 ,
,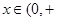 ∞),
∞),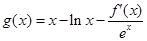 =
=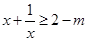 ,
,
所以2-m=1,解得m=1.
(2)由(1)得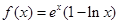 ,得
,得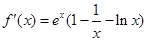 ,令h(x)=
,令h(x)=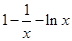 ,则
,则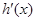 =
= ,
,
当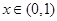 时,
时,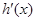 >0,当
>0,当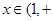 ∞)时,
∞)时,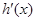 <0,所以h(x)max=h(1)=0.
<0,所以h(x)max=h(1)=0.
又因为ex>0,所以可得当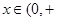 ∞)时,
∞)时,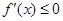 恒成立.故当
恒成立.故当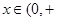 ∞)时,函数
∞)时,函数 单调递减.
单调递减.
因为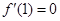 且
且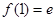 ,所以曲线
,所以曲线 在(1,e)点出的切线方程为y-e=0(x-1),即y=e.
在(1,e)点出的切线方程为y-e=0(x-1),即y=e.
所以直线y=e是曲线f(x)的切线,切点坐标(1,e),且 在
在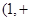 ∞)上单调递减.
∞)上单调递减.
考点:1.求导;2.导数的几何意义;3.导数性质的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
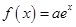 ,
,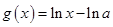 ,其中
,其中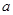 为常数,
为常数,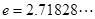 ,函数
,函数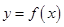 和
和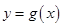 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为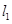 、
、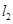 ,且
,且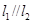 .
. 和
和 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有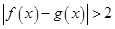 ;
;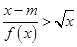 成立,求实数
成立,求实数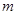 的取值范围.
的取值范围.
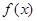 的图象关于原点对称,当
的图象关于原点对称,当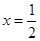 时,
时, ,求
,求 的解析式。
的解析式。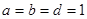 ,
,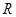 上的单调函数,求
上的单调函数,求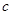 的取值范围
的取值范围 (
(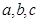 是常数)在
是常数)在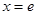 处的切线方程为
处的切线方程为 ,且
,且 .
.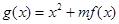 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数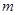 的取值范围;
的取值范围;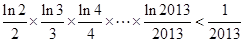 .
.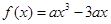 ,
,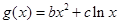 ,且
,且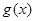 在点(1,
在点(1,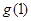 )处的切线方程为
)处的切线方程为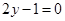 。
。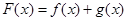 的单调递增区间;
的单调递增区间;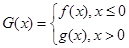 ,若方程
,若方程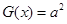 有且仅有四个解,求实数a的取值范围。
有且仅有四个解,求实数a的取值范围。 .
.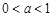 ,试讨论
,试讨论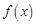 单调性;
单调性; ,当
,当 时,若
时,若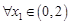 ,存在
,存在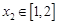 ,使
,使 ,求实数
,求实数 的
的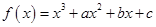 ,曲线
,曲线 在点
在点 处的切线是
处的切线是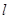 :
:
 ,
,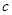 的值;
的值; 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围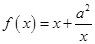 ,
,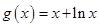 ,其中
,其中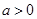 .
.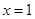 是函数
是函数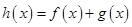 的极值点,求实数
的极值点,求实数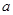 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数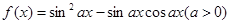 的图象与直线
的图象与直线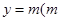 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为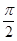
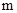 的值;
的值;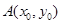 是
是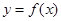 图象的对称中心,且
图象的对称中心,且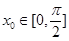 ,求点A的坐标
,求点A的坐标