Question

已知函数f（x）=ax³+

1

2

x²在x=-1处取得极大值，记g（x）=

1

f′(x)

．程序框图如图所示，若输出的结果S=

2013

2014

，则判断框中可以填入的关于n的判断条件是（　　）

A、n≤2013

B、n≤2014

C、n＞2013

D、n＞2014

Answer 1

分析：由已知中函数f（x）=ax³+

1

2

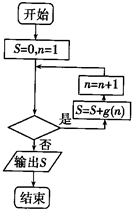
x²在x=-1处取得极大值，可求出a值，进而求出函数f（x）及函数g（x）的解析式，然后利用裂项相消法，可求出g（1）+g（2）+g（3）+…+g（n）的值与n的关系，分析出最后进行循环的循环变量n的终值，分析后可得判断条件．

解答：解：∵函数f（x）=ax³+

1

2

x²在x=-1处取得极大值，
故

3a＞0 f′(-1)=3a-1=0

解得a=

1

3

∴f（x）=

1

3

x³+

1

2

x²，
∴f′（x）=x²+x
∴g（x）=

1

f′(x)

=

1

x2+x

=

1

x

-

1

x+1

∴g（1）+g（2）+g（3）+…+g（n）=（1-

1

2

）+（

1

2

-

1

3

）+…+（

1

n

-

1

n+1

）=1-

1

n+1

=

n

n+1

若输出的结果S=

2013

2014

，
则表示累加的终值应满足n=2013
即n≤2013时，满足进入循环进行累加的条件，n＞2013时退出循环
故选A

点评：根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．