题目内容
己知函数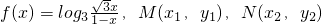 是f(x)图象点的两点,横坐标为
是f(x)图象点的两点,横坐标为 的点P是M,N的中点.
的点P是M,N的中点.
(1)求证:y1+y2的定值;
(2)若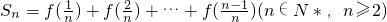 ,
,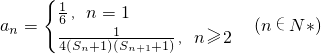 ,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.
,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.
(3)在(2)的条件下,设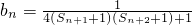 ,Bn为数列{bn}前n项和,证明:
,Bn为数列{bn}前n项和,证明: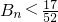 .
.
解:(1)由已知得,x1+x2=1
∴y1+y2=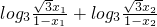 =
=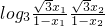
=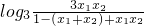 =1
=1
(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1
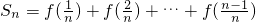 ①
①
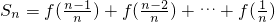 ②
②
①+②得 ,
,
当n≥2时,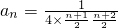 =
=
又当n=1时,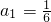 也适合上式,故
也适合上式,故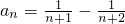
故Tn=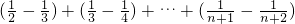 =
=
∵Tn<m(Sn+1+1)对一切n∈N*都成立
即m>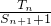 =
=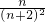 恒成立,
恒成立,
又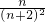 =
=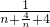
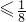 ,
,
所以实数m的取值范围为:( ,+∞)
,+∞)
(3)因为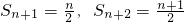 ,
,
所以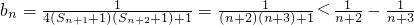
故Bn=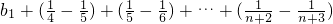
=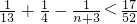
分析:(1)由已知得,x1+x2=1,由对数的计算公式代入可求结果;(2)由y1+y2=f(x1)+f(x2)=1可知,只需用倒序相加法的方式即可求得Sn,进而可得an,Tn,下面由恒成立问题的求法可得;(3)由前面的解答可得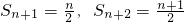 ,代入可得bn,由不等式的放缩法和裂项相消法可证.
,代入可得bn,由不等式的放缩法和裂项相消法可证.
点评:本题为数列的综合应用,涉及函数与不等式的内容,其中列项求和及不等式的放缩法是解决问题的关键,属中档题.
∴y1+y2=
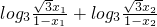 =
=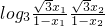
=
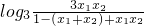 =1
=1(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1
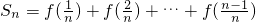 ①
①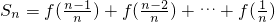 ②
②①+②得
 ,
,当n≥2时,
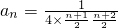 =
=
又当n=1时,
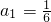 也适合上式,故
也适合上式,故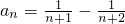
故Tn=
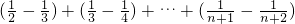 =
=
∵Tn<m(Sn+1+1)对一切n∈N*都成立
即m>
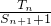 =
=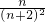 恒成立,
恒成立,又
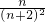 =
=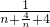
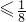 ,
,所以实数m的取值范围为:(
 ,+∞)
,+∞)(3)因为
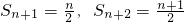 ,
,所以
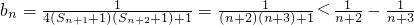
故Bn=
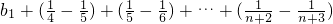
=
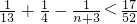
分析:(1)由已知得,x1+x2=1,由对数的计算公式代入可求结果;(2)由y1+y2=f(x1)+f(x2)=1可知,只需用倒序相加法的方式即可求得Sn,进而可得an,Tn,下面由恒成立问题的求法可得;(3)由前面的解答可得
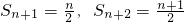 ,代入可得bn,由不等式的放缩法和裂项相消法可证.
,代入可得bn,由不等式的放缩法和裂项相消法可证.点评:本题为数列的综合应用,涉及函数与不等式的内容,其中列项求和及不等式的放缩法是解决问题的关键,属中档题.

练习册系列答案
相关题目