题目内容
已知函数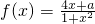 的单调递增区间为[m,n]
的单调递增区间为[m,n]
(1)求证f(m)f(n)=-4;
(2)当n-m取最小值时,点p(x1,y1),Q(x2,y2)(a<x1<x2<n),是函数f(x)图象上的两点,若存在x0使得f′(x0)= ,x求证x1<|x0|<x2.
,x求证x1<|x0|<x2.
解:(1)f′(x)=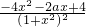 ,
,
依题意,m,n是方程-4x2-2ax+4=0的两根,
∴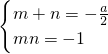 ,
,
f(m)f(n)=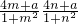
=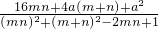
=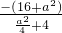 =-4.
=-4.
(2)∵n-m=
= ,
,
∴n-m取最小值时,a=0,n=1,m=-1,
∵f(x)在[-1,1]是增函数,0<x1<x2<1,
∴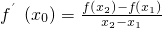 >0,从而x0∈(-1,1).
>0,从而x0∈(-1,1).
f′(x0)=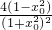 =
= =
=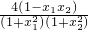 ,
,
即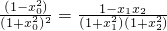 .
.
∵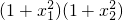 =
=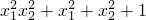
>(x1x2)2+2x1x2+1
=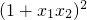 ,
,
∴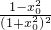 =
=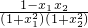 <
< .
.
设g(x)=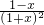 ,则g′(x)=
,则g′(x)=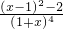 ,
,
∴当x∈(0,1)时,有g′(x)<0,
∴g(x)是(0,1)上的减函数.
∴由g(x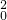 )<g(x1x2),得
)<g(x1x2),得 >x1x2>x
>x1x2>x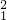 ,∴|x0|>x1.
,∴|x0|>x1.
由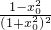 =
=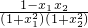 ,及0<1-x
,及0<1-x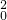 <1-x1x2,
<1-x1x2,
得 <
<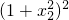 ,
,
故1+ <1+
<1+ ,即|x0|<x2,
,即|x0|<x2,
∴x1<|x0|<x2.
分析:(1)f′(x)=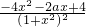 ,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4.
,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4.
(2)由n-m= ,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知
,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知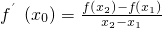 >0,从而x0∈(-1,1).由此入手,结合题设条件能够证明x1<|x0|<x2.
>0,从而x0∈(-1,1).由此入手,结合题设条件能够证明x1<|x0|<x2.
点评:本题考查函数恒成立问题的应用,解题时要注意韦达定理、导数性质、函数单调性、等价转化思想等知识点的合理运用.
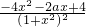 ,
,依题意,m,n是方程-4x2-2ax+4=0的两根,
∴
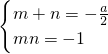 ,
,f(m)f(n)=
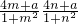
=
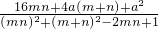
=
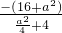 =-4.
=-4.(2)∵n-m=

=
 ,
,∴n-m取最小值时,a=0,n=1,m=-1,
∵f(x)在[-1,1]是增函数,0<x1<x2<1,
∴
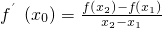 >0,从而x0∈(-1,1).
>0,从而x0∈(-1,1).f′(x0)=
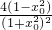 =
= =
=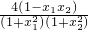 ,
,即
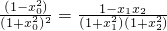 .
.∵
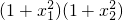 =
=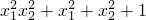
>(x1x2)2+2x1x2+1
=
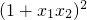 ,
,∴
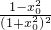 =
=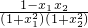 <
< .
.设g(x)=
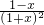 ,则g′(x)=
,则g′(x)=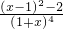 ,
,∴当x∈(0,1)时,有g′(x)<0,
∴g(x)是(0,1)上的减函数.
∴由g(x
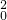 )<g(x1x2),得
)<g(x1x2),得 >x1x2>x
>x1x2>x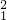 ,∴|x0|>x1.
,∴|x0|>x1.由
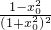 =
=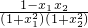 ,及0<1-x
,及0<1-x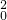 <1-x1x2,
<1-x1x2,得
 <
<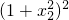 ,
,故1+
 <1+
<1+ ,即|x0|<x2,
,即|x0|<x2,∴x1<|x0|<x2.
分析:(1)f′(x)=
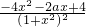 ,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4.
,依题意,m,n是方程-4x2-2ax+4=0的两根,由此能够证明f(m)f(n)=-4.(2)由n-m=
 ,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知
,知n-m取最小值时,a=0,n=1,m=-1,由f(x)在[-1,1]是增函数,0<x1<x2<1,知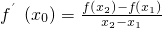 >0,从而x0∈(-1,1).由此入手,结合题设条件能够证明x1<|x0|<x2.
>0,从而x0∈(-1,1).由此入手,结合题设条件能够证明x1<|x0|<x2.点评:本题考查函数恒成立问题的应用,解题时要注意韦达定理、导数性质、函数单调性、等价转化思想等知识点的合理运用.

练习册系列答案
相关题目