Question

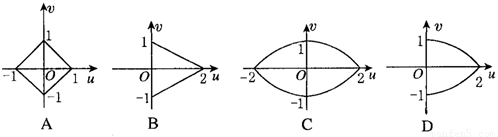
已知正方形OABC的四个顶点O（0，0），A（1，0），B（1，1），C（0，1），设u=2xy，v=x²-y²，是一个由平面xOy到平面uOv上的变换，则正方形OABC在这个变换下的图形是（　　）

• A、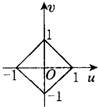
• B、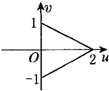
• C、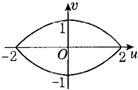
• D、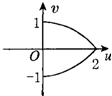

Answer 1

分析：找出正方形的各个顶点变换后的坐标，结合所给的选项，可得结论．

解答：解：根据u=2xy，v=x²-y²，是一个由平面xOy到平面uOv上的变换，
可得点O变为平面uOv上的（0，0）、点A变为平面uOv上的点（0，1）、点B变为平面uOv上的（2，0），点C变为平面uOv上的点（0，-1），
结合所给的选项，D成立．
故选：D．

点评：本题主要考查函数的图象变换，属于基础题．