题目内容
已知函数f(x)=ax-3,g(x)=bx-1+cx-2(a,b∈R)且g(-| 1 | 2 |
(1)试求b,c所满足的关系式;
(2)若b=0,方程f(x)=g(x)在(0,+∞)有唯一解,求a的取值范围;
(3)若b=1,集合A={x|f(x)>g(x),g(x)<0},试求集合A;
分析:(1)且g(-
)-g(1)=f(0)得(-2b+4c)-(b+c)=-3,求出b,c所满足的关系式即可;
(2)由b=0,b-c-1=0,可得c=-1,因为方程f(x)=g(x),即ax-3=-x-2,可化为a=3x-1-x-3,令x-1=t则由题意可得,a=3t-t3在(0,+∞)上有唯一解.令h(t)=3t-t3(t>0),求出h'(t)解出t,分区间讨论函数的增减性,得到函数的极大值,得到a的取值范围即可;
(3)由b=1解出c,则集合A={x|f(x)>g(x)且g(x)<0}={x|ax-3>
且x<0}={x|ax2-3x-1<0且x<0},讨论a的取值来决定A中的元素即可得到A.
| 1 |
| 2 |
(2)由b=0,b-c-1=0,可得c=-1,因为方程f(x)=g(x),即ax-3=-x-2,可化为a=3x-1-x-3,令x-1=t则由题意可得,a=3t-t3在(0,+∞)上有唯一解.令h(t)=3t-t3(t>0),求出h'(t)解出t,分区间讨论函数的增减性,得到函数的极大值,得到a的取值范围即可;
(3)由b=1解出c,则集合A={x|f(x)>g(x)且g(x)<0}={x|ax-3>
| 1 |
| x |
解答: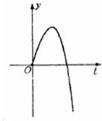 解:(1)由g(-
解:(1)由g(-
)-g(1)=f(0),得(-2b+4c)-(b+c)=-3,
∴b,c所满足的关系式为b-c-1=0.
(2)由b=0,b-c-1=0,可得c=-1,因为方程f(x)=g(x),即ax-3=-x-2,可化为a=3x-1-x-3,令x-1=t
则由题意可得,a=3t-t3在(0,+∞)上有唯一解.
令h(t)=3t-t3(t>0),由h'(t)=3-3t2=0,可得t=1,
当0<t<1时,由h'(t)>0,可知h(t)是增函数;
当t>1时,由h'(t)<0,可知h(t)是减函数,故当t=1时,h(t)取极大值2;
由函数h(t)的图象可在,当a=2或a≤0时,方程f(x)=g(x)有且仅有一个正实数解.
故所求a的取值范围为{a|a=2或a≤0}.
(3)由b=1,b-c-1=0,可得c=0,A={x|f(x)>g(x)且g(x)<0}={x|ax-3>
且x<0}={x|ax2-3x-1<0且x<0},
当a>0时,A=(
,0);
当a=0时,A=(-
,0);
当a<-
时,(△=9+4a<0),A=(-∞,0);
当a=-
时,A={x|x<0且x≠-
};
当-
<a<0时,A=(-∞,
)∪(
,0).
 解:(1)由g(-
解:(1)由g(-| 1 |
| 2 |
∴b,c所满足的关系式为b-c-1=0.
(2)由b=0,b-c-1=0,可得c=-1,因为方程f(x)=g(x),即ax-3=-x-2,可化为a=3x-1-x-3,令x-1=t
则由题意可得,a=3t-t3在(0,+∞)上有唯一解.
令h(t)=3t-t3(t>0),由h'(t)=3-3t2=0,可得t=1,
当0<t<1时,由h'(t)>0,可知h(t)是增函数;
当t>1时,由h'(t)<0,可知h(t)是减函数,故当t=1时,h(t)取极大值2;
由函数h(t)的图象可在,当a=2或a≤0时,方程f(x)=g(x)有且仅有一个正实数解.
故所求a的取值范围为{a|a=2或a≤0}.
(3)由b=1,b-c-1=0,可得c=0,A={x|f(x)>g(x)且g(x)<0}={x|ax-3>
| 1 |
| x |
且x<0}={x|ax2-3x-1<0且x<0},
当a>0时,A=(
3-
| ||
| 2a |
当a=0时,A=(-
| 1 |
| 3 |
当a<-
| 9 |
| 4 |
当a=-
| 9 |
| 4 |
| 2 |
| 3 |
当-
| 9 |
| 4 |
3+
| ||
| 2a |
3-
| ||
| 2a |
点评:本题考查了函数与方程的综合应用,利用换元法转化成二次方程进行求解,利用导数研究函数增减性的能力.

练习册系列答案
相关题目