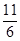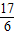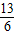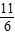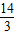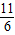题目内容
一质点运动时速度与时间的关系为v(t)=t2-t+2,质点作直线运动,则此物体在时间[1,2]内的位移为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:对速度求定积分求出的是物体的运动位移;利用微积分基本定理求出定积分值即位移.
解答:解:s=
(t2-t+2)dt=(
t3-
t2+2t)
=(
×23-
×22+2×2)-(
-
+2)=
.
故选A
| ∫ | 2 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| | | 2 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 17 |
| 6 |
故选A
点评:本题考查定积分在物理上的应用:对速度求定积分求出的是位移、考查利用微积分基本定理求定积分值.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
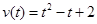 ,质点作直线运动,则此物体在时间
,质点作直线运动,则此物体在时间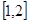 内的位移为( )
内的位移为( )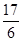 B.
B.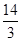 C.
C.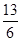
 D.
D.