题目内容
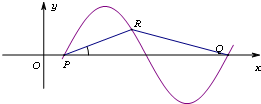（2012•泉州模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| 11 |
| 3 |
3
| ||
| 11 |
（Ⅰ）求函数f（x）的周期；
（Ⅱ）若P的横坐标为1，试求函数y=f（x）的解析式，并求f(
| 4 |
| 3 |
分析：（Ⅰ）在△PRQ中，通过余弦定理求出PQ，推出函数的周期．
（Ⅱ）利用函数的周期求出ω，通过函数f（x）过点P（1，0），求出φ，求出P的纵坐标，求出函数的振幅，推出函数的解析式，然后求解f(
)的值．
（Ⅱ）利用函数的周期求出ω，通过函数f（x）过点P（1，0），求出φ，求出P的纵坐标，求出函数的振幅，推出函数的解析式，然后求解f(
| 4 |
| 3 |
解答：本题满分（13分）．
解：（Ⅰ）在△PRQ中，由余弦定理可得：(3
)2=PQ2+(
)2-2×|PQ|×
×
，
∴PQ2-6|PQ|-16=0，∴|PQ|=8或|PQ|=-2（舍去）．…（3分）
∴函数y=f（x）的周期为8．…．（5分）
（Ⅱ）∵T=8，∴ω=
=
，…．（7分）
又∵函数f（x）过点P（1，0），∴φ=-
，…（9分）
∴f(x)=Asin(
x-
)．
过点R作x轴的垂线，垂足为H，在RT△PHR中，|PR|=
，cos∠RPQ=
，
∴|PH|=3，|RH|=
，R(4，
)，∴Asin(π-
)=
，A=2．…..（11分）
∴f(x)=2sin(
x-
)，
则f(
)=2sin(
-
)=2sin
cos
-2cos
sin
=
．…．（13分）
解：（Ⅰ）在△PRQ中，由余弦定理可得：(3
| 3 |
| 11 |
| 11 |
3
| ||
| 11 |
∴PQ2-6|PQ|-16=0，∴|PQ|=8或|PQ|=-2（舍去）．…（3分）
∴函数y=f（x）的周期为8．…．（5分）
（Ⅱ）∵T=8，∴ω=
| 2π |
| T |
| π |
| 4 |
又∵函数f（x）过点P（1，0），∴φ=-
| π |
| 4 |
∴f(x)=Asin(
| π |
| 4 |
| π |
| 4 |
过点R作x轴的垂线，垂足为H，在RT△PHR中，|PR|=
| 11 |
3
| ||
| 11 |
∴|PH|=3，|RH|=
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∴f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
则f(
| 4 |
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| ||||
| 2 |
点评：本小题主要考查三角函数的图象与性质、两角和与差的三角函数公式以及解三角形等基础知识，考查运算求解能力，考查函数与方程思想、数形结合思想．
练习册系列答案
备战中考寒假系列答案
相关题目