题目内容
(本题满分13分)
在锐角 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,且
,且 ,求
,求 的面积。
的面积。
在锐角
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
.(Ⅰ)求角
 的大小;
的大小;(Ⅱ)若
 ,且
,且 ,求
,求 的面积。
的面积。 (1) ;(2)
;(2)
 ;(2)
;(2)
本试题主要是考核擦了解三角形的运用。
(Ⅰ)利用正弦定理化简已知的等式,根据sinA不为0,可得出sinB的值,由B为锐角,利用特殊角的三角函数值即可求出B的度数;
(Ⅱ)由b及cosB的值,利用余弦定理列出关于a与c的关系式,利用完全平方公式变形后,将a+c的值代入,求出ac的值,将a+c=5与ac=6联立,并根据a大于c,求出a与c的值,再由a,b及c的值,利用余弦定理求出cosA的值,将b,c及cosA的值代入即可求出值.
解:(1)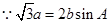
由正弦定理得 所以
所以
因为三角形ABC为锐角三角形,所以
(2)由余弦定理 得
得
 所以
所以 
所以
(Ⅰ)利用正弦定理化简已知的等式,根据sinA不为0,可得出sinB的值,由B为锐角,利用特殊角的三角函数值即可求出B的度数;
(Ⅱ)由b及cosB的值,利用余弦定理列出关于a与c的关系式,利用完全平方公式变形后,将a+c的值代入,求出ac的值,将a+c=5与ac=6联立,并根据a大于c,求出a与c的值,再由a,b及c的值,利用余弦定理求出cosA的值,将b,c及cosA的值代入即可求出值.
解:(1)
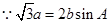
由正弦定理得
 所以
所以
因为三角形ABC为锐角三角形,所以

(2)由余弦定理
 得
得
 所以
所以 
所以


练习册系列答案
相关题目
 =_____
=_____ 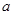 (km), 灯塔A在C北偏东30°,B在C南偏东30°,则A,B之间相距__________。
(km), 灯塔A在C北偏东30°,B在C南偏东30°,则A,B之间相距__________。  ac,则角B=
ac,则角B= B.
B. C.
C. D.
D.

 ,求ΔABC的面积.
,求ΔABC的面积.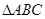 中,已知角
中,已知角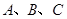 所对的边分别是
所对的边分别是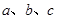 ,边
,边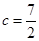 ,
,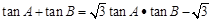 ,又
,又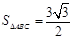 ,求
,求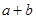 的值。
的值。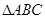 中,已知
中,已知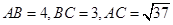 ,则
,则 ,AC=4,则△ABC的面积等于
,AC=4,则△ABC的面积等于  中,已知
中,已知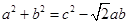 ,则
,则