题目内容
（本小题满分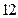
分）已知函数
（
）．
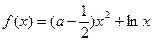（Ⅰ）当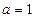
时，求
在区间[1，e]上的最大值和最小值；
（Ⅱ）若在区间（1，+∞）上，函数的图象恒在直线
下方，求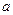
的取值范围．
（1）
，
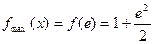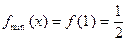；（2）[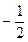
，
]
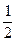解析
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
（本小题满分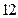分）已知函数（）．
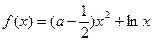（Ⅰ）当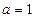时，求在区间[1，e]上的最大值和最小值；
（Ⅱ）若在区间（1，+∞）上，函数的图象恒在直线下方，求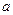的取值范围．
（1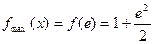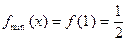），；（2）[，]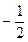
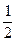解析
阅读快车系列答案
分）已知函数
，
，求该函数的单调递增区间。
分）
的左、 右顶点分别为
，动直线
与圆
相切，且与双曲线左、右两支的交点分别为
.
的取值范围，并求
的最小值；
的斜率为
，直线
的斜率为
，那么，
是定值吗？并证明
分）
与抛物线
相切于点
，且与
轴交于点
，定点
的坐标为
.
满足
，求点
；
（斜率不等于零）与（I）中的轨迹
、
（
与
面积之比的取值范围.
分）
对于任何实数
，y都成立，
；
的值；
为奇函数。
分）
，
的值域。