题目内容
已知关于 的不等式
的不等式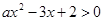 的解集为
的解集为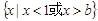 .
.
(1).求实数a,b的值;
(2).解关于 的不等式
的不等式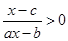 (c为常数).
(c为常数).
(1)a=1,b=2;(2)当c>2时解集为{x|x>c或x<2};当c=2时解集为{x|x≠2,x R};
R};
当c<2时解集为{x|x>2或x<c}.
解析试题分析:(1)根据一元二次方程与一元二次不等式的关系,根据题意可以得到1,b为方程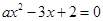 的两根且a>0,根据韦达定理可以得到方程组
的两根且a>0,根据韦达定理可以得到方程组 ,从而求得a=1,b=2;(2)原不等式等价于(x-c)(x-2)>0,根据一元二次不等式的解法,对c进行分类讨论,即可得到当c>2时解集为{x|x>c或x<2};当c=2时解集为{x|x≠2,x
,从而求得a=1,b=2;(2)原不等式等价于(x-c)(x-2)>0,根据一元二次不等式的解法,对c进行分类讨论,即可得到当c>2时解集为{x|x>c或x<2};当c=2时解集为{x|x≠2,x R};当c<2时解集为{x|x>2或x<c}.
R};当c<2时解集为{x|x>2或x<c}.
(1)由题知1,b为方程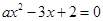 的两根且a>0,即
的两根且a>0,即 , ∴a=1,b=2;
, ∴a=1,b=2;
(2)不等式等价于(x-c)(x-2)>0,
∴当c>2时解集为{x|x>c或x<2};当c=2时解集为{x|x≠2,x R};当c<2时解集为{x|x>2或x<c}.
R};当c<2时解集为{x|x>2或x<c}.
考点:1、一元二次不等式;2、分式不等式转化为一元二次不等式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
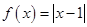 .
.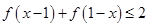 ;
; 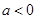 ,求证:
,求证: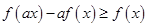
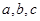 为三角形
为三角形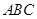 的三边,求证:
的三边,求证: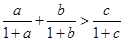
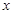 的不等式:
的不等式: 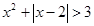
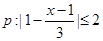 ,
, ,若
,若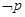 是
是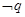 的充分不必要条件,求实数
的充分不必要条件,求实数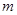 的取值范围.
的取值范围.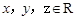 ,且满足:
,且满足: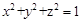 ,
,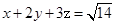 ,求证:
,求证: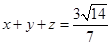 .
.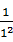 +
+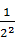 +
+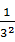 +…+
+…+ <2.
<2.