题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2;数列{bn}的前n项和为Tn , 且满足b1=1,b2=2, ![]() .
.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在正整数n,使得 ![]() 恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
【答案】
(1)解:由Sn=2an﹣2,则当n≥2时,Sn﹣1=2an﹣1﹣2,
两式相减得:an=2an﹣2an﹣1,则an=2an﹣1,
由S1=2a1﹣2,则a1=2,
∴数列{an}是以2为首项,2为公比的等比数列,则an=2n,
由 ![]() .
.
则 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,,
,, ![]() =
= ![]() .
. ![]() =
= ![]()
以上各式相乘, ![]() =
= ![]() ,则2Tn=bnbn+1,
,则2Tn=bnbn+1,
当n≥2时,2Tn﹣1=bn﹣1bn,两式相减得:2bn=bn(bn+1﹣bn﹣1),即bn+1﹣bn﹣1=2,
∴数列{bn}的奇数项,偶数项分别成等差数列,
由 ![]() =
= ![]() ,则b3=T2=b1+b2=3,b1+b3=2b2,
,则b3=T2=b1+b2=3,b1+b3=2b2,
∴数列{bn}是以b1=1为首项,1为公差的等差数列,
∴数列{bn}的通项公式bn=n;
(2)当n=1时, ![]() 无意义,
无意义,
设cn= ![]() =
= ![]() ,(n≥2,n∈N*),
,(n≥2,n∈N*),
则cn+1﹣cn= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
即cn>cn+1>1,
显然2n+n+1>2n﹣(n+1),则c2=7>c3=3>c4>>1,
∴存在n=2,使得b7=c2,b3=c3,
下面证明不存在c2=2,否则,cn= ![]() =2,即2n=3(n+1),
=2,即2n=3(n+1),
此时右边为3的倍数,而2n不可能是3的倍数,故该不等式成立,
综上,满足要求的bn为b3,b7.
【解析】(1)当n≥2时,Sn=2an﹣2,Sn﹣1=2an﹣1﹣2,由an=Sn-Sn-1可得an=2an﹣2an﹣1,则数列{an}是以2为首项,2为公比的等比数列,则an=2n由![]() =
=![]() ,使用累乘法可得到2Tn=bnbn+1,由bn=Tn-Tn-1可得bn+1﹣bn﹣1=2,数列{bn}的奇数项,偶数项分别成等差数列,数列{bn}的通项公式bn=n,(2)设cn=
,使用累乘法可得到2Tn=bnbn+1,由bn=Tn-Tn-1可得bn+1﹣bn﹣1=2,数列{bn}的奇数项,偶数项分别成等差数列,数列{bn}的通项公式bn=n,(2)设cn= ![]() ,作差比较大小,cn>cn+1>1,根据数列的单调性,即可求得存在存在n=2,使得b7=c2,b3=c3.
,作差比较大小,cn>cn+1>1,根据数列的单调性,即可求得存在存在n=2,使得b7=c2,b3=c3.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系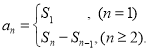 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案