Question

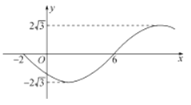
【题目】在平面直角坐标系中，，为，轴上两个动点，点在直线上，且满足，.

（1）求点的轨迹方程；

（2）记点的轨迹为曲线，为曲线与正半轴的交点，、为曲线上与不重合的两点，且直线与直线的斜率之积为，试探究面积的最大值.

Answer 1

【答案】（1）（2）

【解析】

（1）通过引入参数，分别表示点的横纵坐标，得到其参数方程，再消去参数得到其轨迹方程.

（2）按照直线斜率是否存在分两种情况进行讨论，对于斜率存在的情况，通过设出方程，代入曲线消去得到关于的一元二次方程，利用韦达定理，结合题目条件求出m的值，从而求出关于的表达式，再利用基本不等式即可求出最大值.

（1）设，，则，

故点的轨迹方程为

（2）①当直线的斜率不存在时，

设

则，

∴，不合题意.

②当直线的斜率存在时，设

，

联立方程得

则 ，

又

即

将，代入上式得

∴直线过定点，所以直线MN： ，即，

则三角形GMN的底MN上的高为，

∴

令即

∴

当且仅当时取等号

故