题目内容
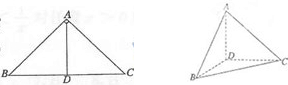 如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是高,沿AD把BC上的△ABD折起,使∠BDC=90°.
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是高,沿AD把BC上的△ABD折起,使∠BDC=90°.(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设BD=1,求三棱柱D-ABC的表面积、体积、内切球半径、外接球半径.
分析:(Ⅰ)注意折叠前后的量的关系,用面面垂直的判定可得:
(Ⅱ)由题意可得三棱锥的棱长,可求得表面积和体积,由等体积的方法可求内切球的半径,把三棱柱D-ABC的外接球转化为正方体的外接球可得答案.
(Ⅱ)由题意可得三棱锥的棱长,可求得表面积和体积,由等体积的方法可求内切球的半径,把三棱柱D-ABC的外接球转化为正方体的外接球可得答案.
解答:解:(Ⅰ)∵折起前AD是BC边上的高,
∴当△ABD折起后,AD⊥DC,AD⊥DB,又DB∩DC=D,
∴AD⊥平面BDC,∵AD?平面ABD,
∴平面ADB⊥平面BDC
(Ⅱ)由题意可知:BD=CD=AD=1,AB=BC=AC=
故三棱柱D-ABC的表面积S=3×
×1×1+
×
×(
)2=
三棱柱D-ABC的体积V=
×
×1×1×1=
设内切球的半径为r,外接球的半径为R,
由等体积的方法可得V=4×
S×r,解得r=
三棱柱D-ABC的外接球的直径为以BA,DB,DC为棱的正方体的体对角线,
故2R=
,解得R=
∴当△ABD折起后,AD⊥DC,AD⊥DB,又DB∩DC=D,
∴AD⊥平面BDC,∵AD?平面ABD,
∴平面ADB⊥平面BDC
(Ⅱ)由题意可知:BD=CD=AD=1,AB=BC=AC=
| 2 |
故三棱柱D-ABC的表面积S=3×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
3+
| ||
| 2 |
三棱柱D-ABC的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
设内切球的半径为r,外接球的半径为R,
由等体积的方法可得V=4×
| 1 |
| 3 |
3-
| ||
| 24 |
三棱柱D-ABC的外接球的直径为以BA,DB,DC为棱的正方体的体对角线,
故2R=
| 3 |
| ||
| 2 |
点评:本题为折叠问题,注意前后的量的关系是解决问题的关键,转化会使问题变得简单,属中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知