题目内容
如图，在五棱锥
中，平面
平面
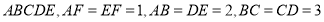，且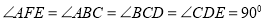
．
（1）已知点
在线段
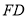上，确定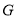
的位置，使得
平面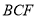
；
（2）点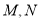
分别在线段
上，若沿直线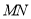
将四边形
向上翻折，
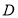与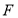
恰好重合，求直线
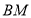与平面
所成角的正弦值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
津桥教育计算小状元系列答案题目内容
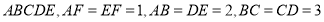如图，在五棱锥中，平面平面，且．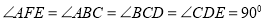
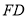（1）已知点在线段上，确定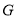的位置，使得平面；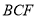
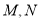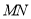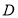（2）点分别在线段上，若沿直线将四边形向上翻折，与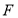恰好重合，求直线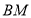与平面所成角的正弦值．
津桥教育计算小状元系列答案
，
满足不等式组
则
的最大值为（ ）
B．
C．
D．
B．
C．
D．
中，“
”是“
、
，
，则动点
的轨迹是（ ）
，则此数列的项数为_______________．
的定义域为___________．
的定义域是（ ）
B.（1，2）