题目内容
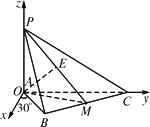
如下图,已知三棱锥P-ABC在某个空间直角坐标系中,![]() =(
=(![]() ,m,0),
,m,0),![]() =(0,2m,0),
=(0,2m,0),![]() =(0,0,2n).
=(0,0,2n).
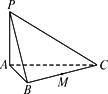
(1)画出这个空间直角坐标系,并指出![]() 与Ox的轴的正方向的夹角;
与Ox的轴的正方向的夹角;
(2)求证:![]() ⊥
⊥![]() ;
;
(3)若M为BC的中点,n=![]() m,求直线AM与平面PBC所成角的大小.
m,求直线AM与平面PBC所成角的大小.
答案:
解析:
解析:
|
(1)解析:如下图,这个坐标系以A为坐标原点O,以AC为Oy轴,以AP所在直线为Oz轴,
(2)证明:∵ ∴ ∴ (3)解析:连AM、PM. ∵| ∴AM⊥BC. 又∵PA⊥BC,∴BC⊥平面PAM. 过A作AE⊥PM于E点,则AE⊥平面PBC, ∴∠AMP为AM与平面PBC所成的角. 又n= |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目