题目内容
(2005
辽宁,17)如下图,已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.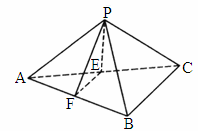
(1)
证明:PC⊥平面PAB;(2)
求二面角P—AB—C的平面角的余弦值;(3)
若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
答案:略
解析:
提示:
解析:
|
解析: (1)证明:连结CF.∵ 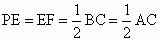 ,∴AP⊥PC. ,∴AP⊥PC.
∵ CF⊥AB,PF⊥AB,∴AB⊥平面PCF.∵ PC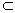 平面PCF,∴PC⊥AB.故PC⊥平面PAB. 平面PCF,∴PC⊥AB.故PC⊥平面PAB.
(2) ∵AB⊥PF,AB⊥CF,∴∠ PFC为所求二面角的平面角.设 AB=a,则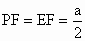 , ,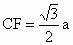 , ,
∴ cos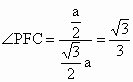 . .
(3) 设PA=x,球半径为R.∵ PC⊥平面PAB,PA⊥PB,故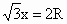 . .
由 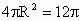 ,得 ,得 ,故x=2, ,故x=2,
∴△ ABC的边长为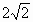 . . |
提示:
|
剖析:本题考查线面垂直、二面角的求法及球与接切三棱锥的问题. |

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目