题目内容
函数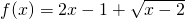 的最小值是
的最小值是
- A.3
- B.4
- C.5
- D.6
A
分析:设 =t,t≥0,则x=t2+2,将原函数式转化为关于t的二次函数式的形式,再利用二次函数的值域求出原函数的值域即可.
=t,t≥0,则x=t2+2,将原函数式转化为关于t的二次函数式的形式,再利用二次函数的值域求出原函数的值域即可.
解答:设 =t,t≥0,则x=t2+2,
=t,t≥0,则x=t2+2,
则函数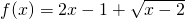 等价于:
等价于:
y=2t2+t+3,t≥0,
∵y=2t2+t+3在[0,+∞)上是增函数,
∴ymin=2×02+0+3=3.
∴函数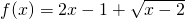 的最小值是3.
的最小值是3.
故选A.
点评:本题主要考查了利用换元法函数的值域,解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法,属于基础题.
分析:设
 =t,t≥0,则x=t2+2,将原函数式转化为关于t的二次函数式的形式,再利用二次函数的值域求出原函数的值域即可.
=t,t≥0,则x=t2+2,将原函数式转化为关于t的二次函数式的形式,再利用二次函数的值域求出原函数的值域即可.解答:设
 =t,t≥0,则x=t2+2,
=t,t≥0,则x=t2+2,则函数
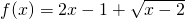 等价于:
等价于:y=2t2+t+3,t≥0,
∵y=2t2+t+3在[0,+∞)上是增函数,
∴ymin=2×02+0+3=3.
∴函数
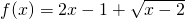 的最小值是3.
的最小值是3.故选A.
点评:本题主要考查了利用换元法函数的值域,解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目