题目内容
下列四个命题中:
(1)如果两个函数都是增函数,那么这两函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].
其中假命题的序号为
(1)如果两个函数都是增函数,那么这两函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].
其中假命题的序号为
(1)、(3)、(4)
(1)、(3)、(4)
.分析:(1)如果两个函数都是增函数,那么这两函数的积运算所得函数为增函数;此命题可以举例说明它是假命题;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;此命题可由奇函数的性质说明它是真命题;
(3)既是奇函数又是偶函数的函数只有一个;此命题可举例说明这样的函数因定义域不同即不是同一个函数,这样的函数有很多;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].此命题的判断可以特例说明它是假命题.
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;此命题可由奇函数的性质说明它是真命题;
(3)既是奇函数又是偶函数的函数只有一个;此命题可举例说明这样的函数因定义域不同即不是同一个函数,这样的函数有很多;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].此命题的判断可以特例说明它是假命题.
解答:解:(1)如果两个函数都是增函数,那么这两函数的积运算所得函数为增函数;考察此命题,它是一个假命题,如两函数y=3x与y=2x在(-∞,0)上都是增函数,但它们的乘积是y=6x2,在 (-∞,0)上是一个减函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;考察此命题,它是一个真命题,由奇函数的性质知,若f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;考察此命题,是一个假命题,因为此函数的解析式只有一个是f(x)=0,但定义域不同时,函数就不是同一个函数,故这样的函数有无穷多个;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].考察此命题,它是一个假命题,因为函数可能是不连续的,如函数y=
综上知(1)、(3)、(4)是假命题
故答案为(1)、(3)、(4)
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;考察此命题,它是一个真命题,由奇函数的性质知,若f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;考察此命题,是一个假命题,因为此函数的解析式只有一个是f(x)=0,但定义域不同时,函数就不是同一个函数,故这样的函数有无穷多个;
(4)若函数的最小值是a,最大值为b,则其值域为[a,b].考察此命题,它是一个假命题,因为函数可能是不连续的,如函数y=
|
综上知(1)、(3)、(4)是假命题
故答案为(1)、(3)、(4)
点评:本题考查命题真假的判断,涉及到函数的单调性,奇函数对称区间上的单调性关系,函数最值与函数值域的关系,解题的关键是理解每个命题,找到针对性的判断方法,本题考查了打理判断的能力,知识覆盖面广,属于基础概念训练题

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
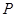 在正方体
在正方体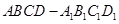 的面对角线
的面对角线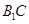 上运动,
上运动,
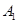
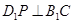 ;
;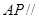 平面
平面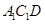 ;
;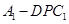 的体积随点
的体积随点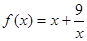 的最小值是6;
的最小值是6;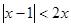 的解集为
的解集为 ;
;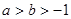 ,则
,则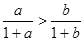 ;
;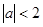 ,
,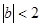 ,则
,则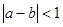 .
.