Question

【题目】已知各项均为正数的数列{an}的前n项和Sn满足S1>1，且(nN*)．

(1)求{an}的通项公式；

(2)设数列满足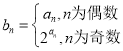，Tn为数列{bn}的前n项和，求Tn；

(3)设*(为正整数)，问是否存在正整数，使得当任意正整数n>N时恒有Cn>2015成立？若存在，请求出正整数的取值范围；若不存在，请说明理由．

Answer 1

【答案】（1）．（2）（3）不存在见解析

【解析】

(1) ，计算得到，，利用公式化简得到，故数列为等差数列，计算得到答案.

(2)讨论为偶数和为奇数两种情况，利用分组求和法计算得到答案.

(3) 不存在，当为奇数时，计算得到，数列单调性递减，得到证明.

（1）时，，且，解得

时，，两式相减得：

即，，

，为等差数列，．

（2），．

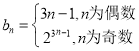当为偶数时，Tn=(b1+b3+…+bn–1)+(b2+b4+…+bn) ,

当为奇数时，Tn=(b1+b3+…+bn)+(b2+b4+…+bn–1)

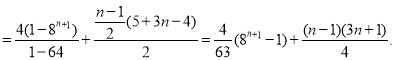
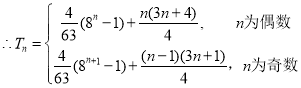
(3),

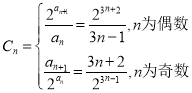当n为奇数时，，

∴Cn+2<Cn，故{Cn}递减， ，

因此不存在满足条件的正整数N．