题目内容

设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
A、
PA
+
PB
=
0
B、
PC
+
PB
=
0
C、
PC
+
PA
=
0
D、
PC
+
PA
+
PB
=
0
分析：以BA，BC为邻边作平行四边形BAMC，利用平行四边形法则可得：
BA
+
BC
=
BM
，已知
BC
+
BA
=2
BP
，得到
BM
=2
BP
，可得点P是对角线的交点．即可得出．
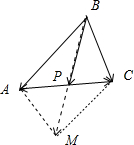
解答：解：如图所示，精英家教网
以BA，BC为邻边作平行四边形BAMC，则
BA
+
BC
=
BM
，
∵
BC
+
BA
=2
BP
，
∴
BM
=2
BP
，可得点P是对角线的交点．
∴
PA
+
PC
=
0
．
故选：C．
点评：本题考查了向量的平行四边形法则、平行四边形的性质，属于基础题．
练习册系列答案
相关题目
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
A、
PA
+
PB
=
0
B、
PC
+
PA
=
0
C、
PB
+
PC
=
0
D、
PA
+
PB
+
PC
=
0
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则
PC
+
PA
=
0
．
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
设P是△ABC所在平面内的一点，且
BC
+
BA
=3
BP
，则（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网