题目内容
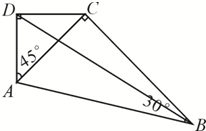如图，将45°直角三角板和30°的直角三角板拼在一起，其中45°直角三角板的斜边与30°直角三角板的30°角所对的直角边重合．若| DB |
| DC |
| DA |
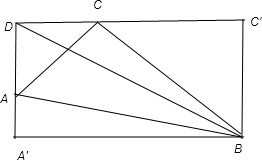
分析：根据直角三角形中的边角关系求出各边长，余弦定理求出DB2=x2+y2 ①，Rt△CC′B中，由勾股定理得 BC2=CC'2+C′B2，即 6=（x-1）2+y2 ②，由①②可解得 x、y值．
解答：解：由题意得，若设 AD=DC=1，则 AC=
，AB=2
，BC=
，由题意知，
=x•
+y•
，
△BCD中，由余弦定理得 DB2=DC2+CB2-2DC•CB•cos（45°+90°）=1+6+2×1×
×
=7+2
，
∵
=x•
+y•
，∠ADC=90°，∴DB2=x2+y2，∴x2+y2=7+2
①．
如图，作
=x
，
=y
，则
=
+
，CC′=x-1，C′B=y，
Rt△CC′B中，由勾股定理得 BC2=CC'2+C′B2，即 6=（x-1）2+y2，②
由①②可得 x=1+
，y=
，故答案为 1+
、
．
| 2 |
| 2 |
| 6 |
| DB |
| DC |
| DA |
△BCD中，由余弦定理得 DB2=DC2+CB2-2DC•CB•cos（45°+90°）=1+6+2×1×
| 6 |
| ||
| 2 |
| 3 |
∵
| DB |
| DC |
| DA |
| 3 |
如图，作
| DC′ |
| DC |
| DA′ |
| DA |
| DB |
| DC′ |
| DA′ |
Rt△CC′B中，由勾股定理得 BC2=CC'2+C′B2，即 6=（x-1）2+y2，②
由①②可得 x=1+
| 3 |
| 3 |
| 3 |
| 3 |
点评：本题考查两个向量的数量积的定义，数量积公式的应用，余弦定理、勾股定理得应用，体现了数形集合的数学思想．
练习册系列答案
相关题目
