题目内容
设函数f(x)=(x-a)2(x+b)ex,a、b∈R,x=a是f(x)的一个极大值点;
(Ⅰ)若a=0,求b的取值范围;
(Ⅱ) 当a是给定的实常数,设x1x2x3是f(x)的3个极值点,问是否存在实数b,可找到x4∈R,使得x1,x2,x3,x4的某种排列x1,x2,x3,x4(其中{i1,i2,i3}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由、
(Ⅰ)若a=0,求b的取值范围;
(Ⅱ) 当a是给定的实常数,设x1x2x3是f(x)的3个极值点,问是否存在实数b,可找到x4∈R,使得x1,x2,x3,x4的某种排列x1,x2,x3,x4(其中{i1,i2,i3}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由、
分析:(I)由函数f(x)=(x-a)2(x+b)ex,我们易求出a=0时,函数的解析式及其导函数的解析式,构造函数g(x)=x2+(b+3)x+2b,结合x=a是f(x)的一个极大值点,我们分析函数g(x)=x2+(b+3)x+2b的两个零点与0的关系,即可确定b的取值范围;
(Ⅱ)由函数f(x)=(x-a)2(x+b)ex,我们易求出f'(x)的解析式,由(I)可得x1、a、x2是f(x)的三个极值点,且x1=
,x2=
,分别讨论x1、a、x2是x1,x2,x3,x4的某种排列构造等差数列时其中三项,即可得到结论.
(Ⅱ)由函数f(x)=(x-a)2(x+b)ex,我们易求出f'(x)的解析式,由(I)可得x1、a、x2是f(x)的三个极值点,且x1=
(a-b-3)-
| ||
| 2 |
(a-b-3)+
| ||
| 2 |
解答:解:(Ⅰ)解:a=0时,f(x)=x2(x+b)ex,∴f'(x)=[x2(x+b)]′ex+x2(x+b)(ex)′=exx[x2+(b+3)x+2b],
令g(x)=x2+(b+3)x+2b,∵△=(b+3)2-8b=(b-1)2+8>0,∴设x1<x2是g(x)=0的两个根,
(1)当x1=0或x2=0时,则x=0不是极值点,不合题意;
(2)当x1≠0且x2≠0时,由于x=0是f(x)的极大值点,故x1<0<x2.∴g(0)<0,即2b<0,∴b<0.
(Ⅱ)解:f'(x)=ex(x-a)[x2+(3-a+b)x+2b-ab-a],
令g(x)=x2+(3-a+b)x+2b-ab-a,则△=(3-a+b)2-4(2b-ab-a)=(a+b-1)2+8>0,
于是,假设x1,x2是g(x)=0的两个实根,且x1<x2.
由(Ⅰ)可知,必有x1<a<x2,且x1、a、x2是f(x)的三个极值点,
则x1=
,x2=
假设存在b及x4满足题意,
(1)当x1,a,x2等差时,即x2-a=a-x1时,
则x4=2x2-a或x4=2x1-a,
于是2a=x1+x2=a-b-3,即b=-a-3.
此时x4=2x2-a=a-b-3+
-a=a+2
或x4=2x1-a=a-b-3-
-a=a-2
(2)当x2-a≠a-x1时,则x2-a=2(a-x1)或(a-x1)=2(x2-a)
①若x2-a=2(a-x1),则x4=
,
于是3a=2x1+x2=
,
即
=-3(a+b+3).
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3<0,于是a+b-1=
,
此时b=-a-
,
此时x4=
=
=-b-3=a+
.
②若(a-x1)=2(x2-a),则x4=
,
于是3a=2x2+x1=
,
即
=3(a+b+3).
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3>0,于是a+b-1=
,
此时b=-a-
此时x4=
=
=-b-3=a+
综上所述,存在b满足题意,
当b=-a-3时,x4=a±2
,
b=-a-
时,x4=a+
,
b=-a-
时,x4=a+
.
令g(x)=x2+(b+3)x+2b,∵△=(b+3)2-8b=(b-1)2+8>0,∴设x1<x2是g(x)=0的两个根,
(1)当x1=0或x2=0时,则x=0不是极值点,不合题意;
(2)当x1≠0且x2≠0时,由于x=0是f(x)的极大值点,故x1<0<x2.∴g(0)<0,即2b<0,∴b<0.
(Ⅱ)解:f'(x)=ex(x-a)[x2+(3-a+b)x+2b-ab-a],
令g(x)=x2+(3-a+b)x+2b-ab-a,则△=(3-a+b)2-4(2b-ab-a)=(a+b-1)2+8>0,
于是,假设x1,x2是g(x)=0的两个实根,且x1<x2.
由(Ⅰ)可知,必有x1<a<x2,且x1、a、x2是f(x)的三个极值点,
则x1=
(a-b-3)-
| ||
| 2 |
(a-b-3)+
| ||
| 2 |
假设存在b及x4满足题意,
(1)当x1,a,x2等差时,即x2-a=a-x1时,
则x4=2x2-a或x4=2x1-a,
于是2a=x1+x2=a-b-3,即b=-a-3.
此时x4=2x2-a=a-b-3+
| (a+b-1)2+8 |
| 6 |
或x4=2x1-a=a-b-3-
| (a+b-1)2+8 |
| 6 |
(2)当x2-a≠a-x1时,则x2-a=2(a-x1)或(a-x1)=2(x2-a)
①若x2-a=2(a-x1),则x4=
| a+x2 |
| 2 |
于是3a=2x1+x2=
3(a-b-3)-
| ||
| 2 |
即
| (a+b-1)2+8 |
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3<0,于是a+b-1=
-9-
| ||
| 2 |
此时b=-a-
7+
| ||
| 2 |
此时x4=
| a+x2 |
| 2 |
| 2a+(a-b-3)-3(a+b+3) |
| 4 |
1+
| ||
| 2 |
②若(a-x1)=2(x2-a),则x4=
| a+x1 |
| 2 |
于是3a=2x2+x1=
3(a-b-3)+
| ||
| 2 |
即
| (a+b-1)2+8 |
两边平方得(a+b-1)2+9(a+b-1)+17=0,∵a+b+3>0,于是a+b-1=
-9+
| ||
| 2 |
此时b=-a-
7-
| ||
| 2 |
此时x4=
| a+x1 |
| 2 |
| 2a+(a-b-3)-3(a+b+3) |
| 4 |
1-
| ||
| 2 |
综上所述,存在b满足题意,
当b=-a-3时,x4=a±2
| 6 |
b=-a-
7+
| ||
| 2 |
1+
| ||
| 2 |
b=-a-
7-
| ||
| 2 |
1-
| ||
| 2 |
点评:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识.

练习册系列答案
相关题目
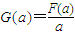 的最小值;
的最小值;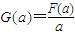 的最小值;
的最小值;