题目内容
先把函数f(x)=sinx-
cosx的图象按向量
=(
,0)平移得到曲线y=g(x),再把曲线y=g(x)上所有点的纵坐标缩短到原来的
倍,横坐标保持不变,得到曲线y=h(x),则曲线y=h(x)的函数表达式( )
| 3 |
| a |
| π |
| 3 |
| 1 |
| 2 |
A、h(x)=sin(x-
| ||
| B、h(x)=sinx | ||
C、h(x)=4sin(x-
| ||
| D、h(x)=4sinx |
分析:先利用两角差的正弦函数进行化简为2sin(x-
),再按向量
=(
,0)右平移后,可确定函数y=g(x),纵坐标缩短到原来的
倍,横坐标保持不变,推出y=h(x),即可.
| π |
| 3 |
| a |
| π |
| 3 |
| 1 |
| 2 |
解答:解:f(x)=2sin(x-
),
按向量
=(
,0)平移后,得到曲线y=g(x)=2sin(x-
)
再把纵坐标缩短到原来的
倍,横坐标保持不变,得到曲线y=h(x)=sin(x-
),
故选A.
| π |
| 3 |
按向量
| a |
| π |
| 3 |
| 2π |
| 3 |
再把纵坐标缩短到原来的
| 1 |
| 2 |
| 2π |
| 3 |
故选A.
点评:本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.注意向量与平移方向的区别,伸长周期变大,缩短周期变小,是基础题.

练习册系列答案
相关题目
 cosx的图象按向量
cosx的图象按向量 =(
=( ,0)平移得到曲线y=g(x),再把曲线y=g(x)上所有点的纵坐标缩短到原来的
,0)平移得到曲线y=g(x),再把曲线y=g(x)上所有点的纵坐标缩短到原来的 倍,横坐标保持不变,得到曲线y=h(x),则曲线y=h(x)的函数表达式
倍,横坐标保持不变,得到曲线y=h(x),则曲线y=h(x)的函数表达式 )
)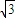 cosx的图象按向量
cosx的图象按向量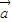 =(
=( ,0)平移得到曲线y=g(x),再把曲线y=g(x)上所有点的纵坐标缩短到原来的
,0)平移得到曲线y=g(x),再把曲线y=g(x)上所有点的纵坐标缩短到原来的 倍,横坐标保持不变,得到曲线y=h(x),则曲线y=h(x)的函数表达式( )
倍,横坐标保持不变,得到曲线y=h(x),则曲线y=h(x)的函数表达式( )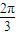 )
)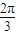 )
)