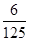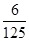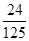题目内容
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为| 4 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| p |
|
a | d |
|
(Ⅱ)求数学期望Eξ.
分析:(I)由题意知事件该生至少有一门课程取得优异成绩与事件“ξ=0”是对立的,要求该生至少有一门课程取得优秀成绩的概率,需要先知道该生没有一门课程优秀,根据对立事件的概率求出结果.
(II)由题意可知,需要先求出分布列中的概率a和b的值,根据互斥事件的概率和相互独立事件同时发生的概率,得到这两个值,求出概率之后,问题就变为求期望.
(II)由题意可知,需要先求出分布列中的概率a和b的值,根据互斥事件的概率和相互独立事件同时发生的概率,得到这两个值,求出概率之后,问题就变为求期望.
解答:解:事件A表示“该生第i门课程取得优异成绩”,i=1,2,3.
由题意可知
P(A1)=
,P(A2)=p,P(A3)=q
(I)由于事件“该生至少有一门课程取得优异成绩”与事件“ξ=0”是对立的,
∴该生至少有一门课程取得优秀成绩的概率是
1-P(ξ=0)=1-
=
(II)由题意可知,
P(ξ=0)=P(
=
(1-p)(1-q)=
,
P(ξ=3)=P(A1A2A3)=
pq=
整理得p=
,q=
.
∵a=P(ξ=1)=P(A1
)+P(
A2
)+P(
A3)
=
(1-p)(1-q)+
p(1-q)+
(1-p)q
=
d=P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
∴Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)+3×P(ξ=3)=
由题意可知
P(A1)=
| 4 |
| 5 |
(I)由于事件“该生至少有一门课程取得优异成绩”与事件“ξ=0”是对立的,
∴该生至少有一门课程取得优秀成绩的概率是
1-P(ξ=0)=1-
| 6 |
| 125 |
| 119 |
| 125 |
(II)由题意可知,
P(ξ=0)=P(
. |
| A1 |
. |
| A2 |
. |
| A3) |
| 1 |
| 5 |
| 6 |
| 125 |
P(ξ=3)=P(A1A2A3)=
| 4 |
| 5 |
| 24 |
| 125 |
整理得p=
| 3 |
| 5 |
| 2 |
| 5 |
∵a=P(ξ=1)=P(A1
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
=
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
=
| 37 |
| 125 |
d=P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
| 58 |
| 125 |
∴Eξ=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)+3×P(ξ=3)=
| 9 |
| 5 |
点评:本题课程互斥事件的概率,相互独立事件同时发生的概率,离散型随机变量的分布列和期望,是一道综合题,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求P,q的值;
(Ⅲ)求数学期望Eξ.
| 4 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| p |
|
a | d |
|
(Ⅱ)求P,q的值;
(Ⅲ)求数学期望Eξ.
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为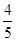 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为 ,
,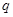 (
( >
>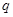 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
|
|
|
|
|
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求 ,
,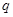 的值;
的值;
(Ⅲ)求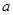 ,
,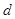 的值.
的值.
(满分12分)某同学参加3门课程的考试.假设该同学第一门课程取得优秀的概率是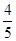 ,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
|
X |
0 |
1 |
2 |
3 |
|
P |
|
a |
b |
|
(1) 求该生至少有1门课程取得优秀成绩的概率;
(2) 求p,q的值;
(3) 求数学期望E(X).