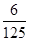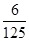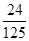题目内容
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为| 4 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| p |
|
a | d |
|
(Ⅱ)求P,q的值;
(Ⅲ)求数学期望Eξ.
分析:(I)由于事件“该生至少有1门课程取得优秀成绩”与事件“ξ=0”是对立的,所以该生至少有1门课程取得优秀成绩的概率为1-P(ξ=0);
(II)根据P(ξ=0)与P(ξ=3)建立关于p和q的方程组,解之即可求出p和q的值;
(III)先求出a和d的值,然后根据Eξ=0×P(ξ=0)+1×P(ξ=1)+2P(ξ=2)+3P(ξ=3)即可求出数学期望.
(II)根据P(ξ=0)与P(ξ=3)建立关于p和q的方程组,解之即可求出p和q的值;
(III)先求出a和d的值,然后根据Eξ=0×P(ξ=0)+1×P(ξ=1)+2P(ξ=2)+3P(ξ=3)即可求出数学期望.
解答:解:事件Ai表示“该生第i门课程取得优秀成绩”,i=1,2,3,由题意知P(A1)=
,P(A2)=p,P(A3)=q
(I)由于事件“该生至少有1门课程取得优秀成绩”与事件“ξ=0”是对立的,所以该生至少有1门课程取得优秀成绩的概率是1-P(ξ=0)=1-
=
,
(II)由题意知P(ξ=0)=P(
)=
(1-p)(1-q)=
P(ξ=3)=P(A1A2A3)=
pq=
整理得 pq=
,p+q=1
由p>q,可得p=
,q=
.
(III)由题意知a=P(ξ=1)=P(A1
)+P(
A2
)+P(
A3)
=
(1-p)(1-q)+
p(1-q)+
(1-p)q=
d=P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
Eξ=0×P(ξ=0)+1×P(ξ=1)+2P(ξ=2)+3P(ξ=3)=
故所求数学期望为
.
| 4 |
| 5 |
(I)由于事件“该生至少有1门课程取得优秀成绩”与事件“ξ=0”是对立的,所以该生至少有1门课程取得优秀成绩的概率是1-P(ξ=0)=1-
| 6 |
| 125 |
| 119 |
| 125 |
(II)由题意知P(ξ=0)=P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
| 1 |
| 5 |
| 6 |
| 125 |
P(ξ=3)=P(A1A2A3)=
| 4 |
| 5 |
| 24 |
| 125 |
整理得 pq=
| 6 |
| 25 |
由p>q,可得p=
| 3 |
| 5 |
| 2 |
| 5 |
(III)由题意知a=P(ξ=1)=P(A1
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
=
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 37 |
| 125 |
d=P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
| 58 |
| 125 |
Eξ=0×P(ξ=0)+1×P(ξ=1)+2P(ξ=2)+3P(ξ=3)=
| 9 |
| 5 |
故所求数学期望为
| 9 |
| 5 |
点评:本题主要考查了互斥事件与对立事件的概念,以及离散型随机变量的期望,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求数学期望Eξ.
| 4 |
| 5 |
| ξ | 0 | 1 | 2 | 3 | ||||
| p |
|
a | d |
|
(Ⅱ)求数学期望Eξ.
某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为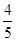 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为 ,
,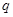 (
( >
>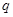 ),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立。记ξ为该生取得优秀成绩的课程数,其分布列为
|
ξ |
0 |
1 |
2 |
3 |
|
|
|
|
|
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求 ,
,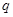 的值;
的值;
(Ⅲ)求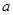 ,
,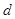 的值.
的值.
(满分12分)某同学参加3门课程的考试.假设该同学第一门课程取得优秀的概率是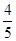 ,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别是p,q(p>q),且不同课程是否取得优秀成绩相互独立,记X为该生取得优秀成绩的课程数,其分布列为
|
X |
0 |
1 |
2 |
3 |
|
P |
|
a |
b |
|
(1) 求该生至少有1门课程取得优秀成绩的概率;
(2) 求p,q的值;
(3) 求数学期望E(X).