Question

8．已知点M是单位圆x²+y²=1上的一个定点，过M作任意两条互相垂直的直线，分别与圆x²+y²=2交于点A、B和C、D，则|AB|+|CD|的最大值是2$\sqrt{6}$．

Answer 1

分析 过O作OH⊥AB，OG⊥CD，垂足分别为H，G，则AB²=4（OB²-OH²），CD²=4（OC²-OG²），利用OH²+OG²=1，可得AB²+CD²=12，根据基本不等式，即可求出|AB|+|CD|的最大值．

解答 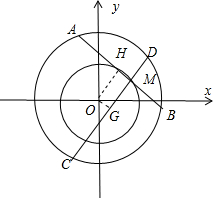解：过O作OH⊥AB，OG⊥CD，垂足分别为H，G，则AB²=4（OB²-OH²），CD²=4（OC²-OG²），
∴AB²+CD²=4（OB²-OH²+OC²-OG²）=4（4-OH²-OG²），
∵OH²+OG²=1
∴AB²+CD²=12，
∴$\frac{AB+CD}{2}$≤$\sqrt{\frac{A{B}^{2}+C{D}^{2}}{2}}$=$\sqrt{6}$，
∴AB+CD≤2$\sqrt{6}$，
∴|AB|+|CD|的最大值是2$\sqrt{6}$．
故答案为：2$\sqrt{6}$．

点评 本题考查直线与圆的位置关系，考查垂径定理的运用，考查基本不等式，属于中档题．