题目内容
如图(1)在等腰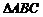 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,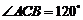 ,现将
,现将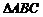 沿CD翻折成直二面角A-DC-B.(如图(2))
沿CD翻折成直二面角A-DC-B.(如图(2))
(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E-DF-C的余弦值;
(III)在线段BC是否存在一点P,但AP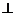 DE?证明你的结论.
DE?证明你的结论.
 |
【答案】
(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF//AB,
又AB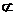 平面DEF,EF
平面DEF,EF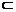 平面DEF,∴AB∥平面DEF.………………4分
平面DEF,∴AB∥平面DEF.………………4分
【解】(Ⅲ)在线段BC上不存在点P,使AP⊥DE,……………………… 9分
证明如下:在图2中, 作AG⊥DE,交DE于G交CD于Q由已知得
∠AED=120°,于是点G在DE的延长线上,从而Q在DC的延长线
上,过Q作PQ⊥CD交BC于P∴PQ⊥平面ACD ∴PQ⊥DE
∴DE⊥平面APQ∴AP⊥DE.但P在BC的延长线上。………………… 12分
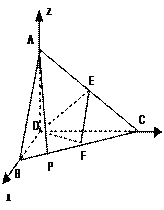
【法二】(Ⅱ)以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,
设CD=a,则AC=BC=2a , AD=DB=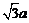 则A(0,0,
则A(0,0,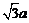 ),B(
),B(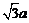 ,0,0),
,0,0),
 C(0,
C(0,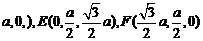 .……………………… 5分
.……………………… 5分
取平面CDF的法向量为 设平面EDF的法向量为
设平面EDF的法向量为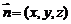 ,
,
则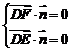 得
得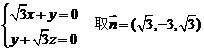 ,…………6分
,…………6分
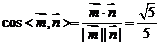 ,……………………………………… 7分
,……………………………………… 7分
所以二面角E—DF—C的余弦值为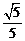 ;…………………………… 8分
;…………………………… 8分
【解】(Ⅲ)设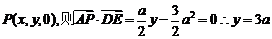 ,
,
又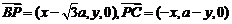 , ……………………………………… 9分
, ……………………………………… 9分
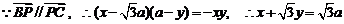 ………………………11分
………………………11分
把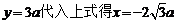 ,可知点P在BC的延长线上
,可知点P在BC的延长线上
所以在线段BC上不存在点P使AP⊥DE.……………………………………………… 12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
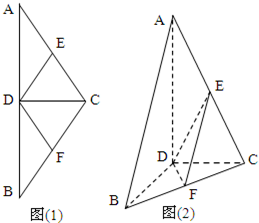 (2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))
(2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))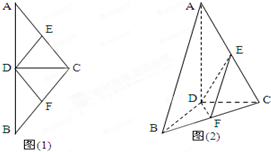 (2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))
(2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))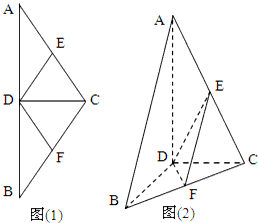 如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))
如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))