题目内容
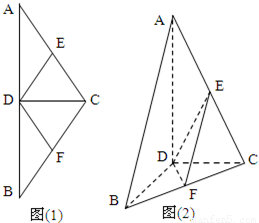
如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E-DF-C的余弦值;
(III)在线段BC是否存在一点P,但AP⊥DE?证明你的结论.

【答案】分析:(I)利用线线平行证明线面平行,由E、F分别是AC、BC中点,得EF∥AB,从而可证AB∥平面DEF;
方法一:(II)取CD的点M,使EM∥AD,过M作MN⊥DF于点N,连接EN,则EN⊥DF,从而可得∠MNE是二面角E-DF-C的平面角,进而可得tan∠MNE=2,从而可得二面角E-DF-C的余弦值;
(Ⅲ)在线段BC上不存在点P,使AP⊥DE,作AG⊥DE,交DE于G交CD于Q由已知得∠AED=120°,于是点G在DE的延长线上,从而Q在DC的延长线上,过Q作PQ⊥CD交BC于P,可得P在BC的延长线上.
方法二(Ⅱ)建立空间直角坐标系,用坐标表示点与向量,求出平面CDF的法向量为 ,平面EDF的法向量为
,平面EDF的法向量为 ,从而可求二面角E-DF-C的余弦值;
,从而可求二面角E-DF-C的余弦值;
(Ⅲ)设P(x,y,0),利用 ,
, ,求得P的坐标,从而可得在线段BC上不存在点P使AP⊥DE.
,求得P的坐标,从而可得在线段BC上不存在点P使AP⊥DE.
解答: 解:(I)如图1在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:(I)如图1在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又AB?平面DEF,EF?平面DEF,∴AB∥平面DEF.
方法一:(II)∵AD⊥CD,BD⊥CD,∴∠ADB是二面角A-CD-B的平面角,∴AD⊥BD,
∴AD⊥平面BCD,
取CD的点M,使EM∥AD,∴EM⊥平面BCD,
过M作MN⊥DF于点N,连接EN,则EN⊥DF,
∴∠MNE是二面角E-DF-C的平面角.
设CD=a,则AC=BC=2a,AD=DB= ,
,
在△DFC中,设底边DF上的高为h
由 ,∴h=
,∴h=
在Rt△EMN中,EM= ,MN=
,MN= h=
h= ,∴tan∠MNE=2
,∴tan∠MNE=2
从而cos∠MNE=
(Ⅲ)在线段BC上不存在点P,使AP⊥DE,
证明如下:在图2中,作AG⊥DE,交DE于G交CD于Q由已知得∠AED=120°,于是点G在DE的延长线上,从而Q在DC的延长线上,过Q作PQ⊥CD交BC于P,∴PQ⊥平面ACD,∴PQ⊥DE,∴DE⊥平面APQ,∴AP⊥DE.
但P在BC的延长线上.
方法二(Ⅱ)如图3以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,
设CD=a,则AC=BC=2a,AD=DB= ,则A(0,0,
,则A(0,0, ),B(
),B( ,0,0),C(0,
,0,0),C(0, .
.
取平面CDF的法向量为 ,设平面EDF的法向量为
,设平面EDF的法向量为 ,
,
则 ,得
,得 取
取 ,
,
∴ ,所以二面角E-DF-C的余弦值为
,所以二面角E-DF-C的余弦值为 ;
;
(Ⅲ)设P(x,y,0),则 ,∴y=3a,
,∴y=3a,
又 ,
,
∵
把 ,可知点P在BC的延长线上
,可知点P在BC的延长线上
所以在线段BC上不存在点P使AP⊥DE.
点评:本题线面平行,考查面面角,考查存在性问题,解题的关键是利用线面平行的判定,确定面面角,同时注意向量方法的运用.
方法一:(II)取CD的点M,使EM∥AD,过M作MN⊥DF于点N,连接EN,则EN⊥DF,从而可得∠MNE是二面角E-DF-C的平面角,进而可得tan∠MNE=2,从而可得二面角E-DF-C的余弦值;
(Ⅲ)在线段BC上不存在点P,使AP⊥DE,作AG⊥DE,交DE于G交CD于Q由已知得∠AED=120°,于是点G在DE的延长线上,从而Q在DC的延长线上,过Q作PQ⊥CD交BC于P,可得P在BC的延长线上.
方法二(Ⅱ)建立空间直角坐标系,用坐标表示点与向量,求出平面CDF的法向量为
 ,平面EDF的法向量为
,平面EDF的法向量为 ,从而可求二面角E-DF-C的余弦值;
,从而可求二面角E-DF-C的余弦值;(Ⅲ)设P(x,y,0),利用
 ,
, ,求得P的坐标,从而可得在线段BC上不存在点P使AP⊥DE.
,求得P的坐标,从而可得在线段BC上不存在点P使AP⊥DE.解答:
 解:(I)如图1在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:(I)如图1在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,又AB?平面DEF,EF?平面DEF,∴AB∥平面DEF.
方法一:(II)∵AD⊥CD,BD⊥CD,∴∠ADB是二面角A-CD-B的平面角,∴AD⊥BD,
∴AD⊥平面BCD,
取CD的点M,使EM∥AD,∴EM⊥平面BCD,
过M作MN⊥DF于点N,连接EN,则EN⊥DF,
∴∠MNE是二面角E-DF-C的平面角.
设CD=a,则AC=BC=2a,AD=DB=
 ,
,在△DFC中,设底边DF上的高为h
由
 ,∴h=
,∴h=
在Rt△EMN中,EM=
 ,MN=
,MN= h=
h= ,∴tan∠MNE=2
,∴tan∠MNE=2从而cos∠MNE=

(Ⅲ)在线段BC上不存在点P,使AP⊥DE,
证明如下:在图2中,作AG⊥DE,交DE于G交CD于Q由已知得∠AED=120°,于是点G在DE的延长线上,从而Q在DC的延长线上,过Q作PQ⊥CD交BC于P,∴PQ⊥平面ACD,∴PQ⊥DE,∴DE⊥平面APQ,∴AP⊥DE.
但P在BC的延长线上.
方法二(Ⅱ)如图3以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,
设CD=a,则AC=BC=2a,AD=DB=
 ,则A(0,0,
,则A(0,0, ),B(
),B( ,0,0),C(0,
,0,0),C(0, .
.取平面CDF的法向量为
 ,设平面EDF的法向量为
,设平面EDF的法向量为 ,
,则
 ,得
,得 取
取 ,
,∴
 ,所以二面角E-DF-C的余弦值为
,所以二面角E-DF-C的余弦值为 ;
;(Ⅲ)设P(x,y,0),则
 ,∴y=3a,
,∴y=3a,又
 ,
,∵

把
 ,可知点P在BC的延长线上
,可知点P在BC的延长线上所以在线段BC上不存在点P使AP⊥DE.
点评:本题线面平行,考查面面角,考查存在性问题,解题的关键是利用线面平行的判定,确定面面角,同时注意向量方法的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
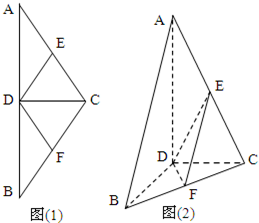 (2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))
(2012•北海一模)如图(1)在等腰△ABC中,D,E,F分别是AB,AC和BC边的中点,∠ACB=120°,现将△ABC沿CD翻折成直二面角A-DC-B.(如图(2))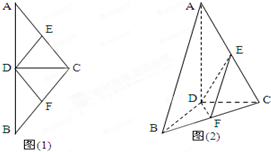 (2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))
(2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))