题目内容
若A,B,C是上不共线的三点,动点P满足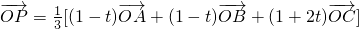 (t∈R且t≠0),则点P的轨迹一定通过△ABC的
(t∈R且t≠0),则点P的轨迹一定通过△ABC的
- A.内心
- B.垂心
- C.外心
- D.AB边的中点
D
分析:根据向量的加法的平行四边形法则向量的运算法则,对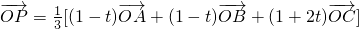 进行化简,取AB的中点D,得到
进行化简,取AB的中点D,得到 ,根据三点共线的充要条件知道P、C、D三点共线,t≠0,则点P的轨迹一定不经过△ABC的重心,但点P的轨迹一定通过△ABC的AB边的中点.
,根据三点共线的充要条件知道P、C、D三点共线,t≠0,则点P的轨迹一定不经过△ABC的重心,但点P的轨迹一定通过△ABC的AB边的中点.
解答:取AB的中点D,则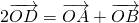
∵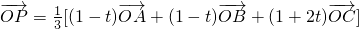
∴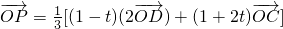
= ,
,
而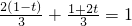 ,
,
∴P、C、D三点共线,
∵t≠0
∴点P的轨迹为直线CD,且不过重心,但一定经过AB的中点D.
故选D.
点评:本小题主要考查向量在几何中的应用、三点共线的充要条件的应用、三角形五心等基础知识,属于基础题.
分析:根据向量的加法的平行四边形法则向量的运算法则,对
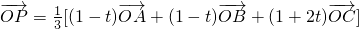 进行化简,取AB的中点D,得到
进行化简,取AB的中点D,得到 ,根据三点共线的充要条件知道P、C、D三点共线,t≠0,则点P的轨迹一定不经过△ABC的重心,但点P的轨迹一定通过△ABC的AB边的中点.
,根据三点共线的充要条件知道P、C、D三点共线,t≠0,则点P的轨迹一定不经过△ABC的重心,但点P的轨迹一定通过△ABC的AB边的中点.解答:取AB的中点D,则
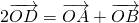
∵
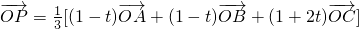
∴
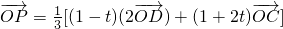
=
 ,
,而
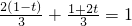 ,
,∴P、C、D三点共线,
∵t≠0
∴点P的轨迹为直线CD,且不过重心,但一定经过AB的中点D.
故选D.
点评:本小题主要考查向量在几何中的应用、三点共线的充要条件的应用、三角形五心等基础知识,属于基础题.

练习册系列答案
相关题目
 (t∈R且t≠0),则点P的轨迹一定通过△ABC的( )
(t∈R且t≠0),则点P的轨迹一定通过△ABC的( )