题目内容
半径为4的球面上有 、
、 、
、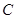 、
、 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )
 、
、 、
、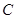 、
、 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )| A.8 | B.16 | C.32. | D.64 |
C
试题分析:视AB,AC,AD为球的内接长方体的一个角,长方体的对角线即为球的直径,设它们的长分别为:a,b,c.故
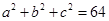 ,计算三个三角形的面积之和,利用基本不等式求最大值。根据题意可知,设AB=a,AC=b,AD=c,则可知AB,AC,AD为球的内接长方体的一个角.设它们的长分别为:a,b,c.故
,计算三个三角形的面积之和,利用基本不等式求最大值。根据题意可知,设AB=a,AC=b,AD=c,则可知AB,AC,AD为球的内接长方体的一个角.设它们的长分别为:a,b,c.故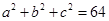
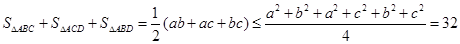
则△
 、△
、△ 、△
、△ 面积之和的最大值为32.故选C.
面积之和的最大值为32.故选C.点评:本题考查了球内接多面体、利用基本不等式求最值问题,考查了同学们综合解决交汇性问题的能力,解答关键是利用构造法求球的直径得到a2+b2+c2=64.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 的三个内角
的三个内角 的对边分别是
的对边分别是 ,且
,且 ,则角
,则角 等于
等于 
 或
或


 60°,如果△ABC 两组解,则x的取值范围( )
60°,如果△ABC 两组解,则x的取值范围( )


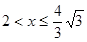
 中,
中,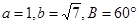 ,则
,则 .
. 的三边之比为3:5:7,求这个三角形的最大角为( )
的三边之比为3:5:7,求这个三角形的最大角为( )



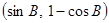 ,向量n =
,向量n =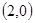 ,且m与n所成角为
,且m与n所成角为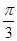 ,其中A、B、C是
,其中A、B、C是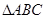 的内角。
的内角。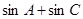 的取值范围。
的取值范围。 分别为
分别为 三个内角
三个内角 的对边,且
的对边,且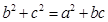 .
. 的大小;
的大小; ,
,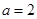 ,求
,求 的面积.
的面积.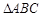 中,角
中,角 、
、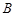 、
、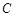 所对应的边分别为
所对应的边分别为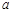 、
、 、
、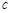 ,且满足
,且满足 .
.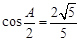 ,求
,求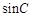 的值.
的值. ,且满足
,且满足 ,
, 的大小;
的大小;  ,求
,求 的取值范围。
的取值范围。