题目内容
函数f（x）=x3+ax2+bx的图象与x轴相切于点（-3，0），且函数存在极值．（I）求函数f（x）的解析式及单调区间；
（II）过函数y=f（x）图象上一点P1（x1，y1）（P1不是y=f（x）图象的对称中心）作曲线的切线，切于不同于P1（x1，y1）的另一点P2（x2，y2），再过P2（x2，y2）作曲线的切线切于不同于P2（x2，y2）的另一点P3（x3，y3），…，过Pn（xn，yn）作曲线的切线切于不同于Pn（xn，yn）的另一点Pn+1（xn+1，yn+1），求xn与xn+1的关系．
分析：（I）对函数求导可得 f′（x）=3x2+2ax+b，由题意可得f（-3）=0，f′（-3）=0，代入可求a，b的值，然后根据导数的符号判断函数的单调区间及极值
（II）可先设切点为（xn+1，yn+1），根据导数的几何意义可得切线方程为y-yn+1=f′（xn+1）（x-xn+1）=（3xn+12+12xn+1+9）（x-xn+1），又切线过点（xn，yn），所以代入切线方程整理求
（II）可先设切点为（xn+1，yn+1），根据导数的几何意义可得切线方程为y-yn+1=f′（xn+1）（x-xn+1）=（3xn+12+12xn+1+9）（x-xn+1），又切线过点（xn，yn），所以代入切线方程整理求
解答：解：（I）f′（x）=3x2+2ax+b
由题意可得f（-3）=0，f′（-3）=0
∴
∴a=6，b=9
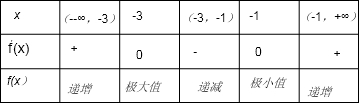
所以f（x）在（-∞，-3），（0，+∞）单调增区间
y极大值=0y极小值=-4
（II）设切点为（xn+1，yn+1）
∴切线方程为y-yn+1=f′（xn+1）（x-xn+1）=（3xn+12+12xn+1+9）（x-xn+1）
又切线过点（xn，yn），所以代入切线方程整理可得：（xn+2xn+1）（x-xn+1）+6（xn-xn+1）=0
∵xn≠nn+1∴xn+2xn+1+6=0
由题意可得f（-3）=0，f′（-3）=0
∴
|
所以f（x）在（-∞，-3），（0，+∞）单调增区间
y极大值=0y极小值=-4
（II）设切点为（xn+1，yn+1）
∴切线方程为y-yn+1=f′（xn+1）（x-xn+1）=（3xn+12+12xn+1+9）（x-xn+1）
又切线过点（xn，yn），所以代入切线方程整理可得：（xn+2xn+1）（x-xn+1）+6（xn-xn+1）=0
∵xn≠nn+1∴xn+2xn+1+6=0
点评：利用导数的符号变化求解函数的单调区间及函数的极值是函数在导数部分最基本的考查，而切线方程的求解关键是要熟练应用导数的几何意义．
练习册系列答案
相关题目