题目内容
【题目】如图,已知三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
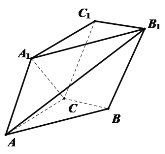
(1)证明:![]()
![]() ;
;
(2)设![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连结![]() .由菱形得对角线垂直,再由已知及面面垂直的性质定理得线面垂直
.由菱形得对角线垂直,再由已知及面面垂直的性质定理得线面垂直![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,从而
,从而![]() ,于是证得线面垂直后再得线线垂直;
,于是证得线面垂直后再得线线垂直;
(2)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,证得
,证得![]() 与
与![]() 都垂直后,以
都垂直后,以![]() 为原点,
为原点,![]() 为正方向建立空间直角坐标系,写出各点坐标,求出平面的法向量,则法向量夹角得二面角,注意要判断二面角是锐角还是钝角.
为正方向建立空间直角坐标系,写出各点坐标,求出平面的法向量,则法向量夹角得二面角,注意要判断二面角是锐角还是钝角.
(1)连结![]() .
.
∵![]() ,四边形
,四边形![]() 为菱形,∴
为菱形,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]()
![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]()
![]()
(2)取![]() 的中点为
的中点为![]() ,连结
,连结![]() .
.
∵![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,∴
,∴![]() ,
,![]() .
.
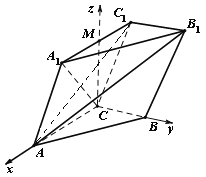
又由(1)知![]() ,以
,以![]() 为原点,
为原点,![]() 为正方向建立空间直角坐标系,如图.
为正方向建立空间直角坐标系,如图.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() (0,0,0),
(0,0,0),![]() (1,0,
(1,0,![]() ),
),![]() (2,0,0),
(2,0,0),![]() (0,1,0),
(0,1,0),![]() (-1,1,
(-1,1,![]() ).
).
由(1)知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,∴
,∴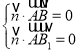 .
.
∵![]() ,
,![]() ,∴
,∴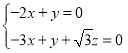 .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
∴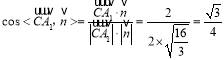 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]()

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米,该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元平方米):
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根据表格数据,完成下列茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数;
A户型 | B户型 | |
2. | ||
3. | ||
4. |
(2)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会,小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格,为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
【题目】某农科所为改良玉米品种,对已选出的一组玉米的茎高进行统计,获得茎叶图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
抗倒伏 | 易倒伏 | 总计 | |
矮茎 | |||
高茎 | |||
总计 |
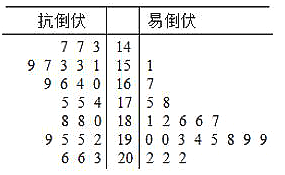
(1)请完成以上![]() 列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
(2)为改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,则选取的植株均为矮茎的概率是多少?
参考公式: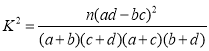 (其中
(其中![]() )
)
参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |