题目内容
 (2012•上高县模拟)为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数是6.
(2012•上高县模拟)为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频数是6.(Ⅰ)估计该校高三学生质检数学成绩在125~140分之间的概率,并求出样本容量;
(Ⅱ)从样本中成绩在65~95分之间的学生中任选两人,求至少有一人成绩在65~80分之间的概率.
分析:(Ⅰ)由比例关系可得分布在[125,140]上的概率,由频率=
可得答案;
(Ⅱ)由题意可得:样本中成绩在[65,80)和[80,95)上的学生分别有2人、4人,分别记为x,y;a,b,c,d.利用列举法可得答案.
| 频数 |
| 样本容量 |
(Ⅱ)由题意可得:样本中成绩在[65,80)和[80,95)上的学生分别有2人、4人,分别记为x,y;a,b,c,d.利用列举法可得答案.
解答:解:(Ⅰ)估计该校高三学生质检数学成绩在125~140之间的概率p1=
=
,(2分)
又设样本容量为m,则
=
,解得,m=40.(4分)
(Ⅱ)样本中成绩在65~8(0分)之间的学生有
×40=2人,记为x,y;
成绩在80~9(5分)之间的学生
×40=4人,记为a,b,c,d,(5分)
从上述6人中任选2人的所有可能情形有:{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},{y,b},{y,c},{y,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},共15种,(8分)
至少有1人在65~8(0分)之间的可能情形有{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},{y,b},{y,c},{y,d},共9种,(11分)
因此,所求的概率p2=
=
.(12分)
| 3 |
| 1+2+6+8+3 |
| 3 |
| 20 |
又设样本容量为m,则
| 6 |
| m |
| 3 |
| 20 |
(Ⅱ)样本中成绩在65~8(0分)之间的学生有
| 1 |
| 20 |
成绩在80~9(5分)之间的学生
| 2 |
| 20 |
从上述6人中任选2人的所有可能情形有:{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},{y,b},{y,c},{y,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},共15种,(8分)
至少有1人在65~8(0分)之间的可能情形有{x,y},{x,a},{x,b},{x,c},{x,d},{y,a},{y,b},{y,c},{y,d},共9种,(11分)
因此,所求的概率p2=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查古典概型的求解和频率分布的结合,列举对事件是解决问题的关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
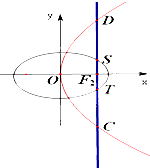 (2012•上高县模拟)如图,椭圆
(2012•上高县模拟)如图,椭圆