题目内容
集合 ,集合
,集合
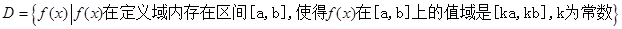 .
.
(1)当 时,判断函数
时,判断函数 是否属于集合
是否属于集合 ?并说明理由.若是,则求出区间
?并说明理由.若是,则求出区间 ;
;
(2)当 时,若函数
时,若函数
 ,求实数
,求实数 的取值范围;
的取值范围;
(3)当 时,是否存在实数
时,是否存在实数 ,当
,当 时,使函数
时,使函数
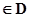 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
 ,集合
,集合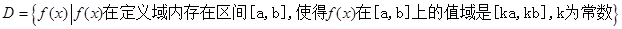 .
.(1)当
 时,判断函数
时,判断函数 是否属于集合
是否属于集合 ?并说明理由.若是,则求出区间
?并说明理由.若是,则求出区间 ;
;(2)当
 时,若函数
时,若函数
 ,求实数
,求实数 的取值范围;
的取值范围;(3)当
 时,是否存在实数
时,是否存在实数 ,当
,当 时,使函数
时,使函数
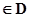 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.解: (1)函数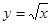 属于集合
属于集合 ,且这个区间是
,且这个区间是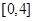
(2) ;
;
(3)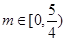
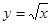 属于集合
属于集合 ,且这个区间是
,且这个区间是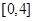
(2)
 ;
;(3)
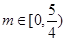
本试题主要是考查了函数的定义域和值域,以及二次方程中韦达定理的运用
(1)根据新定义,得到定义域和值域间的对应关系式,解方程得到。
(2)设出函数,根据新定义,可知函数的定义域和值域,那么利用关系得到参数的范围。
(3)假设存在实数m,满足题意,那么利用a,b的不等关系讨论得到结论
(1)根据新定义,得到定义域和值域间的对应关系式,解方程得到。
(2)设出函数,根据新定义,可知函数的定义域和值域,那么利用关系得到参数的范围。
(3)假设存在实数m,满足题意,那么利用a,b的不等关系讨论得到结论

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
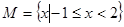 ,
,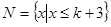 ,若
,若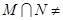 Æ.则实数
Æ.则实数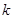 的取值范围是 .
的取值范围是 . ,
, 和
和 都是全集
都是全集 的子集,且有
的子集,且有 ,
, ,
, ,求集合
,求集合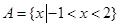 ,集合
,集合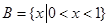 ,则有( )
,则有( )





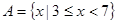 ,
,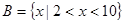 ,
,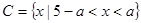 .
. 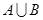 ,
,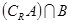 ; (2) 若
; (2) 若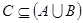 ,求
,求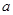 的取值范围.
的取值范围. 为给定的实数,那么集合
为给定的实数,那么集合 的非空真子集的个数为( )
的非空真子集的个数为( )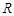 的函数
的函数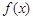 对任意实数
对任意实数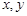 满足:
满足: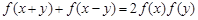 ,且
,且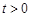 使
使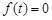 ,给出下列结论:①
,给出下列结论:①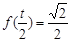 ;②
;②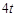 ;④
;④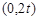 内为单调函数。其中正确命题的序号是___________。
内为单调函数。其中正确命题的序号是___________。 |
| },N={
},N={ },则M
},则M  N= ( )
N= ( )
 的真子集共有( )
的真子集共有( )