题目内容
已知定义域为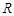 的函数
的函数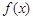 对任意实数
对任意实数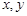 满足:
满足: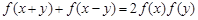 ,且
,且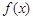 不是常值函数,常数
不是常值函数,常数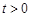 使
使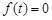 ,给出下列结论:①
,给出下列结论:①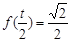 ;②
;②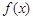 是奇函数;③
是奇函数;③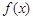 是周期函数且一个周期为
是周期函数且一个周期为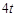 ;④
;④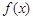 在
在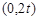 内为单调函数。其中正确命题的序号是___________。
内为单调函数。其中正确命题的序号是___________。
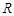 的函数
的函数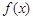 对任意实数
对任意实数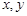 满足:
满足: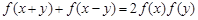 ,且
,且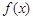 不是常值函数,常数
不是常值函数,常数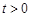 使
使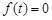 ,给出下列结论:①
,给出下列结论:①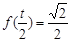 ;②
;②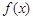 是奇函数;③
是奇函数;③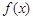 是周期函数且一个周期为
是周期函数且一个周期为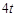 ;④
;④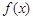 在
在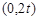 内为单调函数。其中正确命题的序号是___________。
内为单调函数。其中正确命题的序号是___________。.③
解:根据题意,在f(x+y)+f(x-y)=2f(x)f(y)中,
令y=0可得,2f(x)=2f(x)f(0),又由f(x)不是常函数,即f(x)=0不恒成立,则f(0)=1,
依次分析4个命题可得:
对于①、在f(x+y)+f(x-y)=2f(x)f(y)中,令x=y=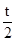
,可得f(t)+f(0)=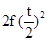
结合f(0)=1,f(t)=0,可得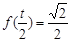 ,则可得
,则可得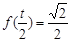 ,故①错误,
,故①错误,
对于②、在f(x+y)+f(x-y)=2f(x)f(y)中,令x=0,可得f(y)+f(-y)=2f(0)f(y)=2f(y),f(y)+f(-y)=0不恒成立,f(x)不是奇函数,故②错误,
对于③、在f(x+y)+f(x-y)=2f(x)f(y)中,令y=t可得,在f(x+t)+f(x-t)=2f(x)f(t)=0,
即f(x+t)=-f(x-t),则f(x+3t)=-f(x+t)=f(x-t),即f(x+3t)=f(x-t),则f(x)是周期函数且一个周期为4t,③正确,
对于④、根据题意,无法判断f(x)的单调性,则④错误;
故答案为③.
令y=0可得,2f(x)=2f(x)f(0),又由f(x)不是常函数,即f(x)=0不恒成立,则f(0)=1,
依次分析4个命题可得:
对于①、在f(x+y)+f(x-y)=2f(x)f(y)中,令x=y=
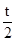
,可得f(t)+f(0)=
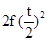
结合f(0)=1,f(t)=0,可得
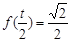 ,则可得
,则可得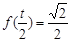 ,故①错误,
,故①错误,对于②、在f(x+y)+f(x-y)=2f(x)f(y)中,令x=0,可得f(y)+f(-y)=2f(0)f(y)=2f(y),f(y)+f(-y)=0不恒成立,f(x)不是奇函数,故②错误,
对于③、在f(x+y)+f(x-y)=2f(x)f(y)中,令y=t可得,在f(x+t)+f(x-t)=2f(x)f(t)=0,
即f(x+t)=-f(x-t),则f(x+3t)=-f(x+t)=f(x-t),即f(x+3t)=f(x-t),则f(x)是周期函数且一个周期为4t,③正确,
对于④、根据题意,无法判断f(x)的单调性,则④错误;
故答案为③.

练习册系列答案
相关题目
 ,集合
,集合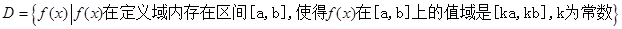 .
. 时,判断函数
时,判断函数 是否属于集合
是否属于集合 ?并说明理由.若是,则求出区间
?并说明理由.若是,则求出区间 ;
;
 ,求实数
,求实数 的取值范围;
的取值范围; 时,是否存在实数
时,是否存在实数 ,当
,当 时,使函数
时,使函数
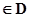 ,若存在,求出
,若存在,求出 ,其中
,其中 ,
, ,求实数
,求实数 的取值范围.
的取值范围. ,
,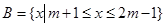 ,若
,若 ,求
,求 的取值范围。
的取值范围。 A)∩B,(C
A)∩B,(C ,
, ,
, ,求
,求 .
. ,求实数a的取值范围.
,求实数a的取值范围.
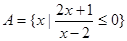 ,集合B是
,集合B是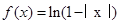 的定义域,
的定义域, B .
B .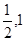 ] B、 (-1,2]
] B、 (-1,2] 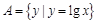 ,
,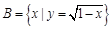 ,则A∩B为( )
,则A∩B为( )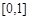



 ,
, ,则集合Q不可能是( )
,则集合Q不可能是( )

 >
>
