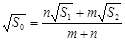题目内容
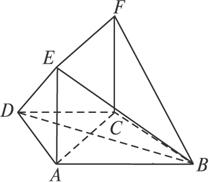
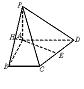
如图在梯形ABCD中,AD∥BC,∠ABC=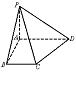
且∠ADC=arcsin![]() ,又PA⊥平面ABCD,PA=a.
,又PA⊥平面ABCD,PA=a.
求(1)二面角P—CD—A的大小(用反三角函数表示).
(2)点A到平面PBC的距离.
答案:
解析:
解析:
| 解:(1)如图,在平面ABCD内,过点A作AE⊥CD,垂足为E,连接PE.
由PA⊥平面ABCD,由三垂线定理知PE⊥CD,故∠PEA是二面角P—CD—A的平面角. 在Rt△DAE中,AD=3a,∠ADC=arcsin 则AE=AD·sinADE= 在Rt△PAE中,tanPEA= 故二面角P—CD—A的大小为arctan (2)在平面PAB中,过点A作AH⊥PB,垂足为H. 由PA⊥平面ABCD,AB⊥BC,PA⊥BC,则有BC⊥平面PAB,又AH 因此,线段AH的长即为点A到平面PBC的距离. 在等腰直角△PAB中,AH= |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
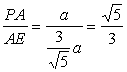

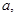
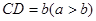 。若
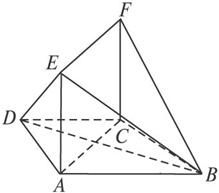
。若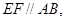 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为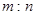 ,则可推算出:
,则可推算出: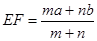 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设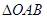 ,
,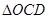 的面积分别为
的面积分别为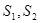 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为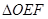 的面积
的面积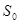 与
与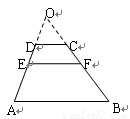
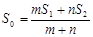 B.
B.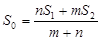
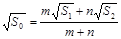 D.
D.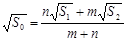
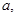
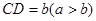 。若
。若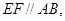 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为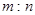 ,则可推算出:
,则可推算出: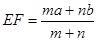 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设 ,
,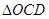 的面积分别为
的面积分别为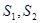 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为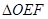 的面积
的面积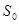 与
与
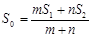 B
B
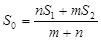
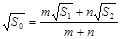 D
D