题目内容
(2006
上海模拟)设S为满足下列两个条件的实数所构成的集合:① ,②若
,②若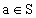 ,则
,则 ,求解下列问题:
,求解下列问题:
(1)
若数列 中的项都在S中,求S中所含元素个数最少的集合
中的项都在S中,求S中所含元素个数最少的集合 ;
;
(2)
在 中任取3个元素a,b,c,求使abc=-1的概率;
中任取3个元素a,b,c,求使abc=-1的概率;
(3)S
中所含元素个数一定是 个吗?若是,请给出证明;若不是,试说明理由.
个吗?若是,请给出证明;若不是,试说明理由.
答案:略
解析:
解析:
|
解析: (1) 所以 所以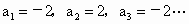
即集合 S中必有2和-2.
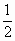 .同理,由 .同理,由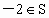 可得 可得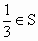 和 和 .所以S中至少含有元素 .所以S中至少含有元素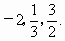 即S中所含元素个数最少的集合为 即S中所含元素个数最少的集合为 . .
(2) 在 任取3个元素a、b、c,共有(组合) 任取3个元素a、b、c,共有(组合) 种取法,而abc=-1的只有 种取法,而abc=-1的只有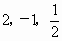 和 和 两种取法,所以使abc=-1的概率为 两种取法,所以使abc=-1的概率为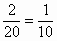 . .
(3) 一定是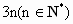 个. 个.
由 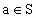 且 且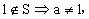
所以由  即当 即当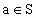 时, 时, 下面证明 下面证明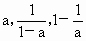 互不相等.若 互不相等.若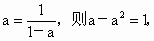 即 即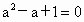 无解,所以 无解,所以 .若 .若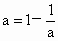 ,则 ,则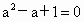 无解,所以 无解,所以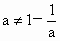 ,若 ,若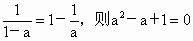 无解,所以 无解,所以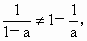 即 即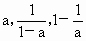 互不相等.所以S中含有元素个数一定是 互不相等.所以S中含有元素个数一定是 个. 个. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
