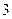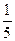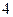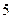题目内容
已知|a|＜1,|b|＜1,|c|＜1,求证: abc+2＞a+b+c.
证明略
设线段的方程为y=f(x)=(bc－1)x+2－b－c,其中|b|＜1,|c|＜1,|x|＜1,且－1＜a＜1。
∵f(－1)=1－bc+2－b－c=(1－bc)+(1－b)+(1－c)＞0
f(1)=bc－1+2－b－c=(1－b)(1－c)＞0
∴线段y=(bc－1)x+2－b－c(－1＜x＜1)在x轴上方，
这就是说，当|a|＜1,|b|＜1,|c|＜1时，恒有abc+2＞a+b+c.
∵f(－1)=1－bc+2－b－c=(1－bc)+(1－b)+(1－c)＞0
f(1)=bc－1+2－b－c=(1－b)(1－c)＞0
∴线段y=(bc－1)x+2－b－c(－1＜x＜1)在x轴上方，
这就是说，当|a|＜1,|b|＜1,|c|＜1时，恒有abc+2＞a+b+c.
练习册系列答案
相关题目
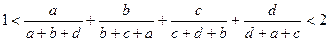
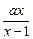＜1的解集为{x|x＜1或x＞2},那么a的值为__________.
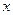的一元二次方程
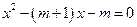有两个不相等的实数根，求
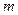的取值范围．
件某种商品花去
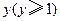元，第二次再买这种商品发现该商品已降价，且
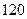件恰好降价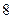
元，第二次比第一次多买
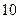件，共花去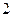
元，那么他第一次至少买这种商品几件？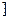
－2,2
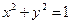,则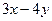
的最大值是 ( )
