题目内容
已知函数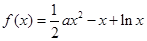 (
(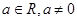 )
)
(1)当 时,求曲线
时,求曲线 在
在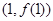 处的切线方程;
处的切线方程;
(2)若在区间 上函数
上函数 的图象恒在直线
的图象恒在直线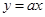 下方,求
下方,求 的取值范围.
的取值范围.
(1)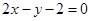 ;(2)
;(2)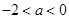
解析试题分析:(1)先求导函数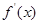 ,由导数的几何意义知
,由导数的几何意义知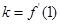 ,利用直线的点斜式方程求切线方程;(2)由题意,不等式
,利用直线的点斜式方程求切线方程;(2)由题意,不等式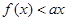 恒成立,对于恒成立问题可考虑参变分离,也可以构造函数法,本题构造函数
恒成立,对于恒成立问题可考虑参变分离,也可以构造函数法,本题构造函数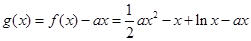 ,等价于
,等价于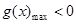 ,故利用导数求函数
,故利用导数求函数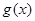 的最大值,求
的最大值,求 的根,得
的根,得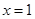 或
或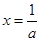 ,讨论根的大小并和定义域比较,同时要注意分子二次函数的开口方向,通过判断函数大致图像,从而求函数的最大值,进而列不等式求
,讨论根的大小并和定义域比较,同时要注意分子二次函数的开口方向,通过判断函数大致图像,从而求函数的最大值,进而列不等式求 的取值范围.
的取值范围.
试题解析:(1)函数的定义域为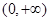 .
.
当 时,
时,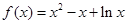 ,
,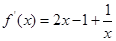 ,则
,则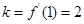 ,又切点为
,又切点为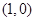 ,故曲线
,故曲线 在
在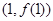 处的切线方程为
处的切线方程为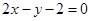 .
.
(2)令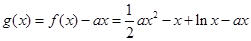 定义域
定义域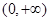
在区间 上,函数
上,函数 的图象恒在直线
的图象恒在直线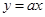 下方,等价于
下方,等价于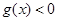 在
在 恒成立,即
恒成立,即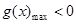 ,
,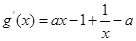
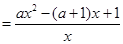
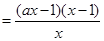 ,令
,令 ,得
,得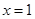 或
或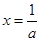 ,
,
当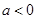 时,
时,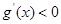 ,故
,故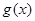 在
在 单调递减,则
单调递减,则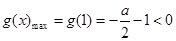 ,得
,得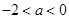 ;
;
当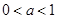 时,
时,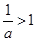 ,当
,当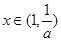 时,
时,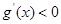 ,
,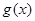 单调递减;当
单调递减;当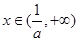 时,
时,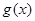 单调递增,此时
单调递增,此时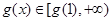 ,故不可能
,故不可能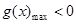 ,不合题意;
,不合题意;
当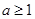 时,
时,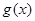 在
在 单调递增,
单调递增,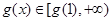 ,故不可能
,故不可能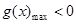 ,不合题意.
,不合题意.
综上: 的取值范围
的取值范围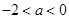 .
.
考点:1、导数的几何意义;2、导数在单调性上的应用;3、利用导数求函数的极值、最值.

练习册系列答案
相关题目
 在
在 时取得极小值.
时取得极小值. 的值;
的值;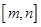 ,使得
,使得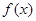 在该区间上的值域为
在该区间上的值域为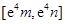 ?若存在,求出
?若存在,求出 ,
,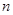 的值;
的值;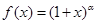 的定义域是
的定义域是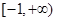 ,其中常数
,其中常数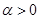 .
.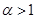 ,求
,求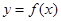 的过原点的切线方程.
的过原点的切线方程.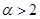 时,求最大实数
时,求最大实数 ,使不等式
,使不等式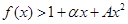 对
对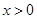 恒成立.
恒成立.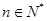 ,有
,有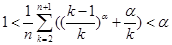 .
.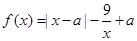 ,
,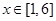 ,
,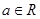 .
.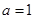 ,试判断并用定义证明函数
,试判断并用定义证明函数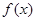 的单调性;
的单调性;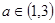 时,求函数
时,求函数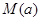 .
. ,
, .
. 在其定义域上为增函数,求
在其定义域上为增函数,求 的取值范围;
的取值范围;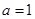 时,函数
时,函数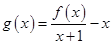 在区间
在区间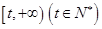 上存在极值,求
上存在极值,求 的最大值.
的最大值.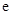 ≈
≈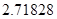 ).
).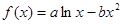 图像上一点
图像上一点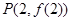 处的切线方程为
处的切线方程为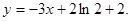 (1)求
(1)求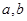 的值;(2)若方程
的值;(2)若方程 在区间
在区间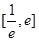 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令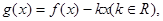 如果
如果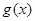 的图像与
的图像与 轴交于
轴交于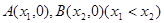 两点,
两点,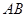 的中点为
的中点为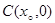 ,求证:
,求证: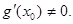
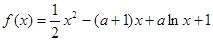
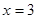 是
是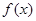 的极值点,求
的极值点,求 的范围,使得
的范围,使得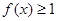 恒成立.
恒成立.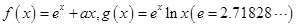 ..
..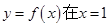 处的切线为
处的切线为 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为 ,求a的值;
,求a的值;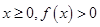 恒成立,试确定
恒成立,试确定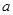 的取值范围;
的取值范围;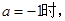 是否存在实数
是否存在实数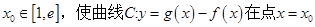 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出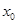 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.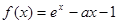
 的单调增区间
的单调增区间 内单调递增,求
内单调递增,求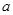 的取值范围.
的取值范围.